Подсчет времени движения частицы несжимаемой жидкости вдоль линии тока

Для однородной несжимаемой жидкости в выражениях характеристической функции потока F (z), потенциальной функции φ и функции тока ψможно опустить постоянный множитель r и вести расчеты применительно к объемному дебиту Q и скорости фильтрации u, а не к массовым дебиту Gи скорости фильтрации ru.Таким образом формулы (7.40) для проекции массовой скорости фильтрации на оси декартовых координат могут быть для несжимаемой жидкости применены к вычислению проекции скорости фильтрации на эти оси u_x и u_y:

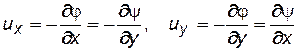. (7.73)

Формула (7.41) для несжимаемой жидкости запишется в виде:

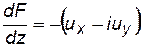. (7.74)

Но проекции скорости движения на оси координат равны dx/dt и dy/dt,следовательно, можно записать

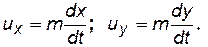(7.75)

Исключаем из (7.73) u_x и u_y с помощью (7.75) и интегрируя, получим уравнения движения частицы в направлении осей x и у :

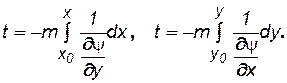(7.76)

Чтобы вывести формулу времени движения частицы жидкости вдоль линии тока 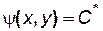,подставим значения u_x и u_yиз (7.75) в формулу (7.74):

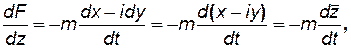(7.77)

где `z=x-iy - сопряженное с z комплексное переменное.

Разделяя переменные в (7.77) и интегрируя вдоль линии тока, получим формулу для подсчета времени движения частицы на длине кривой L:

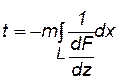. (7.78)