Относительное количество нефти, остающейся в пласте к моменту
Начала обводнения скважин кольцевой батареей
| а/rн. | Число скважин | ||
| ∞ | |||
| Относительная величина площади ωн/pа2 | |||
| 0,4 | 1,84 | 1,33 | |
| 0,1 | 1,99 | 1,33 |
Метод конформного отображения
Общие положения
Ранее была установлена связь между теорией функций комплексного переменного и теорией плоских фильтрационных потоков.
Эта связь позволяет каждую функцию F (z) комплексного переменного z = х +iy трактовать, как поле некоторого плоского движения.
Введем новое комплексное переменное 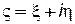 , связанное со старым переменным z соотношением z = z (ς), где z (ς) произвольная аналитическая функция.
, связанное со старым переменным z соотношением z = z (ς), где z (ς) произвольная аналитическая функция.
Первое движение происходило на плоскости комплексного переменного z и характеризовалось комплексным потенциалом F (z). Подставляя вместо zего выражение через ς получим
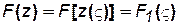 , (7.94)
, (7.94)
где F1 –новая функция.
Полученная из F функция F1 определяет некоторый плоский фильтрационный поток на плоскости ς и, изучив первый поток F, можно легко изучить поток F1 (ς).
Таким образом, задаваясь той или иной преобразующей функцией z = z (ς), из одного потока F (z) плоскости z можно получить бесчисленное множество других потоков на плоскости ς. Последнееозначает, что функция z=z(ς) реализует конформное отображение плоскости zна плоскость ς.
Для решения задач интерференции скважин в качестве исходного потока удобно взять течение к скважине, эксцентрично расположенной в круговом пласте, являющееся вместе с тем течением между равнодебитными источником и стоком.
Применение метода конформного отображения позволяет получить решения ряда задач интерференции скважин значительно быстрее, нежели методами, основанными на прямой суперпозиции источников и стоков.
Метод конформных отображений в настоящее время широко применяется во многих физических и технических задачах. При помощи этого метода удается решить ряд плоских задач напорной и безнапорной фильтраций.
Дата добавления: 2020-03-17; просмотров: 728;











