Вывод некоторых формул для притока к скважинам при помощи конформного отображения

<40 41 424344 45 46 >

Предположим, что на плоскости комплексного переменного z=х+iy дано некоторое течение с комплексным потенциалом F(z).Введем новое комплексное переменное 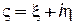, связанное со старым переменным z зависимостью z=z(ς) или ς=ς(z).Отделяя в функции z=z(ς)действительную часть от мнимой, получаем

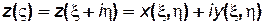откуда x=x(ξ,η), y=y(ξ,η),

ξ= ξ(x,y), η= η(x,y).(7.95)

Уравнения (7.95) устанавливают соответствие между точками плоскостей ς и z. В зависимости от того, однозначна или многозначна преобразующая функция z=z(ς), каждой точке плоскости ς соответствует одна или несколько точек плоскости z.

Точно так же каждой линии одной плоскости соответствует одна или несколько линий на другой плоскости. Таким образом, линиям тока и эквипотенциалям, т. е. сетке течения одной плоскости, будет соответствовать вполне определенная сетка течения на другой плоскости. При этом, сами значения потенциала скорости Ф и функции тока Ψбудут одинаковыми на соответствующих друг другу линиях обеих плоскостей. Производная dz/dς,–есть также некоторая функция комплексного переменного, вполне определенная в соответствующих друг другу точках обеих плоскостей z и ς. Это означает по самому определению производной, что предел отношения

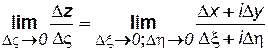
не зависит от закона стремления к нулю отрезков Δξ и Δη. Отсюда следует, что в каждой точке плоскости ς и соответствующей (или соответствующих) ей точке плоскости zотношение соответствующих бесконечно малых отрезков dz и dς постоянно. Но из каждой точки плоскости ς можно провести бесконечное множество отрезков dς₁, dς₂, ... Им будут соответствовать на плоскости z бесконечно малые отрезки dς₁, dς₂, ... также исходящие из точки плоскости z, соответствующей рассматриваемой точке плоскости ς .

Так как 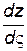в каждой точке есть вполне определённая величина, то 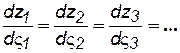(7.96)

Из (7.96) следует пропорция .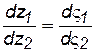

Аргумент дроби равен разности аргументов числителя и знаменателя. Но argdz₁ – это угол между направлениями элемента dz_l и осью х.

Таким образом,

arg dz_l - arg dz₂ = arg dς₁ - arg dς₂,

т. е. углы между отрезками dz₁, dz₂ и отрезками dς₁, dς₂равны.

Поэтому преобразование z(ς) или ς (z) называется конформным, так как оно сохраняет подобие бесконечно малых элементов в соответствующих точках.

Доказательство сохранения дебитов скважины при конформном отображении. Пусть на плоскости z имеется скважина радиусом r_с., на плоскости ς ей будет соответствовать скважина радиусом r_с. При этом, так как радиусы скважин обеих плоскостей можно считать очень малыми по сравнению с размерами областей течения, то на основании формулы (7.96)

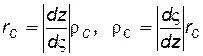. (7.97)

Покажем теперь, что при конформном отображении дебиты скважин – стоков или источников – сохраняются на обеих плоскостях. Для этого окружим скважину на плоскости z произвольным замкнутым контуром l, которому на плоскости ς будет соответствовать также замкнутый контур λ. Пусть dn и dl – элементы нормали и касательной для контура l на плоскости z и соответственно dv и d λ – для контура λ на плоскости ς.

Тогда абсолютная величина дебита |Q |скважины на плоскости zвыразится интегралом по замкнутому контуру

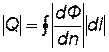, (7.98)

так как 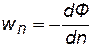составляющая скорости фильтрации по нормали к контуру.

Но по смыслу конформного преобразования, сохраняющего подобие бесконечно малых элементов в соответствующих точках обеих плоскостей, согласно формуле (7.96) имеем

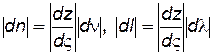. (7.99)

Подставляя эти выражения в формулу (7.98), получаем

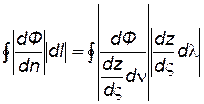Сокращая на 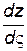будем иметь

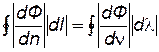. (7.100)

В правой части формулы (7.100) согласно формуле (7.98) стоит абсолютная величина дебита скважины на плоскости ς, равная абсолютному значению дебита скважины на плоскости z.

Связь прямолинейно-параллельного и плоско-радиального течений. За исходный поток примем простейший вид прямолинейно-параллельного течения

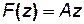. (7.101)

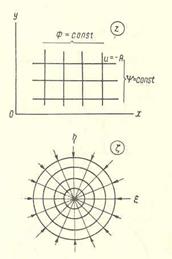
Рис.7.26. Соответствие между эквипотенциалями и линиями тока

Пусть А – положительная и действительная постоянная. Отделяя действительную и мнимую части, получаем

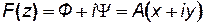откуда

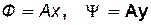. (7.102)

Т. о. эквипотенциали Ф=Ах=const являются семейством прямых, параллельных оси у (рис. 7.26.), а линии тока Ψ = Ау = const – прямыми, параллельными оси х.

Проекции скорости фильтрации u,v равны

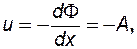. (7.103)

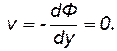
Таким образом, характеристическая функция течения F (z) = Az определяет прямолинейно-параллельное течение в сторону отрицательной оси х с постоянной во всех точках скоростью u = - А.

Сделаем замену переменного

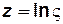,(7.104)

где .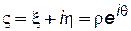

Здесь r, θ – полярные координаты на плоскости ς.

Тогда

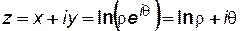, (7.105)

откуда, сравнивая действительные и мнимые части, получим

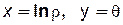. (7.106)

Прямым линиям х = const плоскости zсоответствуют на плоскости ς кривые lnr=const, r= const, т. е. окружности с центром в начале координат, а прямым у=const –лучи θ = const плоскости ς(рис. 7.26.).

Следовательно, сетке течения Ф = Ах = const, Ψ = Ay = const на плоскости zсоответствует на плоскости ς сетка течения r= const иθ = const, т. е. при А >0 – приток к точечному стоку в начале координат с дебитом q = 2 pА.

Приток к скважине в пласте с прямолинейным контуром питания. Возьмем за исходный поток приток к точечному стоку на плоскости ς:

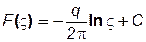, (7.107)

где С– произвольная константа.

Пусть на плоскости z в точке х = 0, у = а находится скважина малого радиуса г_с, причем ось хявляется одной эквипотенциалью Ф=Ф_к, а окружность малого радиуса г_с – другой эквипотенциалью Ф = Ф_с (рис. 7.27). На плоскости z мы имеем приток к скважине в полубесконечном пласте с прямолинейным контуром питания.

Если удастся найти преобразование ς = ς (z) или обратное z=z (ς), которое реализует конформное отображение верхней полуплоскости z в круг r = r_к плоскости ς, а точку z_c = ia плоскости z, где расположен центр скважины радиусом r_с, в начало координат ς=0 плоскости ς, то задача будет решена.

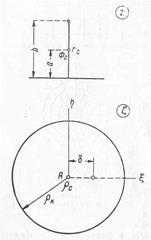
Рис. 7.27. Соответствие между плоскостями z и ς в задаче о притоке в скважину

В нашем случае искомое преобразование имеет вид:

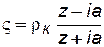. (7.108)

Действительно, полагая z=ia, из формулы (7.108) получаем ς=0, т. е. центру скважины на плоскости z соответствует начало координат ς= 0на плоскости ς.

Точки вещественной оси х плоскости z переходят в точки окружности r = r_к плоскости ς. Действительно, полагая в формуле (7.108) z = х – любому вещественному числу, имеем

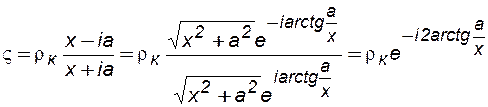,. (7.109)

откуда следует .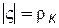

Таким образом, действительная ось z = х перешла в окружность ρ_н плоскости ς, а точка верхней полуплоскости z = ia в начало координат ς = 0. Отсюда ясно, что формула (7.108) и есть нужное нам преобразование. Радиусы скважин обеих плоскостей согласно формуле (7.97) связаны соотношением .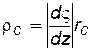

Отсюда согласно (7.108) получаем

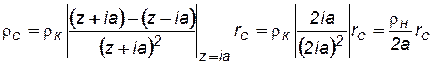. (7.110)

Для комплексного потенциала на плоскости z получаем

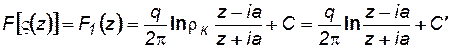, (7.111)

где С' – новая константа, равная

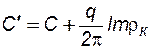. (7.112)

Для дебита, согласно формуле Дюпюи, имеем 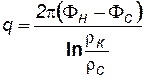. Подставляя сюда ρ_с из формулы (7.110), получим

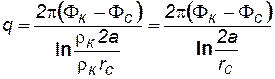. (7.113)

ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ

1. Основные виды задач по заданию режима работы скважин.

2. Сущность метода суперпозиции.

3. Потенциал сложного потока.

4. Уравнения эквипотенциальных поверхностей.

5. Метод отображения источников и стоков.

6. Фильтрационный поток от нагнетательной скважины к эксплуатационной (выражение для потенциала, изобара, поле течения).

7. Фильтрационный поток от нагнетательной скважины к эксплуатационной (выражение для массового дебита, модуль массовой скорости, время и площадь обводнения).

8. Приток к группе скважин с удаленным контуром питания.

9. Приток к скважине в пласте с прямолинейным контуром питания.

10. Приток к скважине, расположенной вблизи непроницаемой прямолинейной границы.

11. Приток к скважине в пласте с произвольным контуром питания.

12. Приток к скважинам кольцевой батареи (дебит скважины и батареи). Что такое – эксцентрично расположенная скважина?

13. Приток к скважинам кольцевой батареи (поле течения, оценки эффекта взаимодействия).

14. Приток к прямолинейной батарее скважин (конечное число скважин). В чем отличие формул Голосова для четного и нечетного числа скважин?

15. Приток к прямолинейной батарее скважин (бесконечное число скважин).

16. Метод Борисова (сущность, внутреннее и внешнее сопротивления).

17. Интерференция несовершенных скважин.

18. Взаимодействие скважин в анизотропном пласте (батарея расположена во внутренней неоднородности кругового пласта).

19. Взаимодействие скважин в неоднородно проницаемом и анизотропном пластах (батарея расположена во внешней неоднородности кругового пласта).