Вычисление тройных интегралов.

Пример. Вычислить интеграл 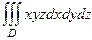где D куб .

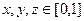Решение. Здесь 3 вложенных действия: .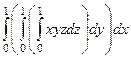

Сначала вычислим первообразную по 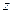и применим формулу Ньютона-Лейбница по , = .

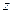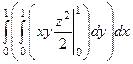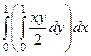После этого вычислим первообразную по :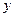

= = = = .

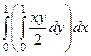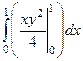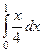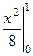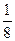Замечание. Тройные интегралы тоже могут быть по сложной области, а не параллелепипеду или кубу. Во внутреннем интеграле (по переменной 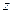) в этом случае может быть зависимость уже от обеих внешних переменных, а именно .

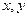Пример. Вычислить интеграл 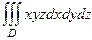где D трёхмерное тело над квадратом 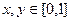, ограниченное сверху плоскостью .

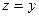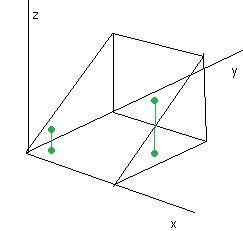
Решение. В проекции на горизонтальную плоскость это тот же квадрат, что и в прошлом примере, а вот высота во внутреннем интеграле по 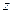теперь не от 0 до 1, а от 0 до 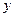, и тогда получается: 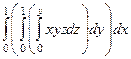= = 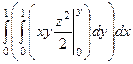= = 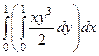= = 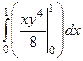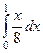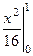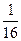. Ответ. .

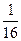Приложения кратных интегралов.Если 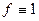то при вычислении интеграла получится просто площадь области D (если двойной интеграл) или объём области (если тройной интеграл). Физический смысл: если плотность равна 1, то масса как раз и равна объёму. Для сравнения, для определённых интегралов было то же самое, только там получалась длина отрезка: .

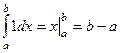Приложения:

1) Вычисление площадей фигур (двойной интеграл).

Допустим, надо вычислить площадь области под графиком 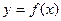, если 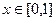. Если записать интеграл в виде 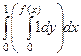то он преобразуется к = .

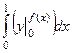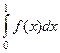Как видим, двойной интеграл почти сразу же превращается в обычный определённый, после того, как во внутреннем интеграле вычисляется первообразная от 1 по переменной 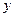. То есть, с помощью двойного интеграла или с помощью определённого - методы практически эквивалентны.

2) Вычисление объёмов тел (тройной интеграл).

Аналогично, если 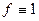, то с помощью тройного интеграла получается объём тела.

3) Площадь поверхности.

Формула площади явно заданной поверхности:

.

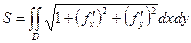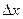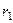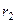Доказательство. Разобьём область определения на прямоугольники небольшого размера, со сторонами и . Над таким прямоугольником есть часть поверхности, за счёт малости размера она очень близка к касательной плоскости. Рассмотрим параллелограмм на касательной плосоксти и вычислим его площадь. Его стороны это векторы и . Рассмотрим подробнее, какие у них координаты.

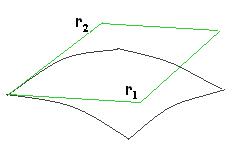
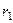направлен по касательной в сечении, параллельном оси 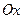, то есть тангенс угла наклона для него это 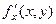. Тогда его координаты: 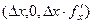= 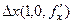. Аналогично вектор 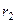расположен в сечении вдоль оси 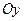, его координаты 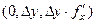, если вынести дельта, то это 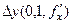. Площадь параллелограмма вычисляется с помощью векторного произведения, она равна модулю векторного произведения (вспомните 1 семестр, векторная алгебра и геометрия).

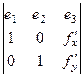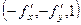= , модуль этого вектора: .

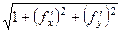Вспомним, что мы вынесли за скобку коэффициенты 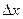и 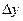. Поэтому

в интегральных суммах получается 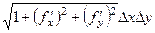. Тогда при переходе к пределу, будет интеграл: 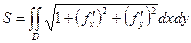, где D это область определения в горизонтальной плоскости (то есть область, над которой расположена поверхность).