Абсолютная сходимость.
Если 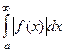 сходится, то сходимость интеграла
сходится, то сходимость интеграла 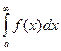 называется абсолютной, а если сходится только
называется абсолютной, а если сходится только 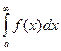 , а
, а 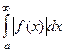 расходится, тоусловной.
расходится, тоусловной.
Сходимость в смысле главного значения.Рассмотрим функцию, заданную на всей числовой оси. Если предел
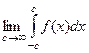 существует и является конечным числом, то интеграл называется сходящимся «в смысле главного значения». Это понятие необходимо потому, что бывают ситуации, когда интегралы
существует и является конечным числом, то интеграл называется сходящимся «в смысле главного значения». Это понятие необходимо потому, что бывают ситуации, когда интегралы 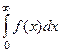 и
и 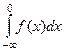 оба расходятся, причём один равен
оба расходятся, причём один равен 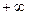 , другой
, другой 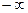 , а данный предел по симметричным интервалам существует. Так, если функция нечётна, то
, а данный предел по симметричным интервалам существует. Так, если функция нечётна, то 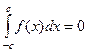 для любого числа
для любого числа 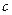 .
.
Кратные интегралы.
Определение. Пусть дана функция 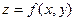 , её область определения - некоторая область D в плоскости. Введём разбиение D на части двумя семействами прямых линий. В каждой части
, её область определения - некоторая область D в плоскости. Введём разбиение D на части двумя семействами прямых линий. В каждой части 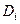 возьмём произвольную точку
возьмём произвольную точку 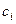 с координатами
с координатами 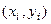 . Площадь
. Площадь 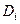 обозначим
обозначим 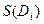 . Величина
. Величина 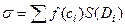 называется интегральной суммой. Предел этой величины при измельчении разбиения называется двойным интегралом функции
называется интегральной суммой. Предел этой величины при измельчении разбиения называется двойным интегралом функции 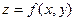 по множеству
по множеству 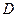 , и обозначается
, и обозначается 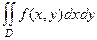 .
.
Как правило, сначала мы будем рассматривать область D - прямоугольник: 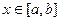 ,
, 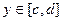 , затем произвольные области.
, затем произвольные области.
Геометрический смысл. Интегральная сумма означает сумму объёмов параллелепипедов, построенных на каждом из оснований 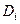 , а интеграл - объём под поверхностью, которая задана уравнением
, а интеграл - объём под поверхностью, которая задана уравнением 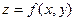 .
.
Физический смысл.Если функция задаёт плотность какой-либо плоской пластины, то двойной интеграл - масса.
Аналогично определяется понятие тройного интеграла. Если дана функция 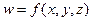 , определённая в трёхмерной области, то её можно разбить на части с помощью трёх семейств плоскостей, выбрать по точке в каждой части, и составить интегральную сумму. То, что получается в пределе, называется тройным интегралом.
, определённая в трёхмерной области, то её можно разбить на части с помощью трёх семейств плоскостей, выбрать по точке в каждой части, и составить интегральную сумму. То, что получается в пределе, называется тройным интегралом. 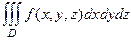 . Физический смысл тройного интеграла: если функция - плотность некоторой породы, то в результате вычисления тройного интеграла получится масса.
. Физический смысл тройного интеграла: если функция - плотность некоторой породы, то в результате вычисления тройного интеграла получится масса.
Метод вычисления.При вычислении кратных интегралов, как двойных, так и тройных, сводят к так называемым «повторным» интегралам.
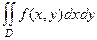 =
= 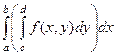 . Также в этом случае можно применять запись вида:
. Также в этом случае можно применять запись вида: 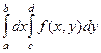 где дифференциал пишется именно после того интеграла, которому он соответствует. При фиксировании одной переменной, мы получаем функцию уже не двух, а одной переменной. Так, при
где дифференциал пишется именно после того интеграла, которому он соответствует. При фиксировании одной переменной, мы получаем функцию уже не двух, а одной переменной. Так, при  получается
получается 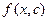 . На чертеже этому соответствует сечение поверхности вдоль оси
. На чертеже этому соответствует сечение поверхности вдоль оси 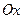 , то есть кривая. Интеграл по одной переменной при фиксированной второй, это площадь криволинейной трапеции, которая получается в сечении.
, то есть кривая. Интеграл по одной переменной при фиксированной второй, это площадь криволинейной трапеции, которая получается в сечении.
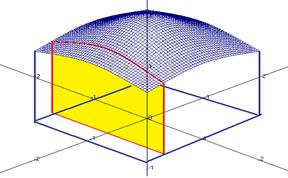
Если проинтегрировать все эти величины по второму направлению, то получится объём тела под поверхностью. Аналогично, как если разрезали бы булку хлеба на очень тонкие слои, а затем вычислили площадь каждого, и сложили все эти величины (умножая на их толщину) получили бы объём.
Пример. Вычислить интеграл 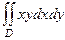 , где
, где 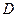 есть квадрат:
есть квадрат: 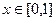 ,
, 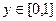 .
.
Решение. 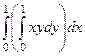 =
= 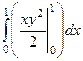 вычислили сначала «частную первообразную» по переменной
вычислили сначала «частную первообразную» по переменной 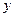 , то есть ту функцию, частная производная от которой по
, то есть ту функцию, частная производная от которой по 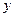 была бы
была бы 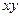 . Во внутренних скобках применяем формулу Ньютона-Лейбница по переменной
. Во внутренних скобках применяем формулу Ньютона-Лейбница по переменной 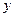 .
.
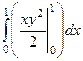 =
= 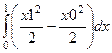 =
= 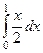 . Оставшийся интеграл по переменной
. Оставшийся интеграл по переменной 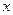 вычисляется обычным образом:
вычисляется обычным образом: 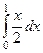 =
= 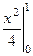 =
= 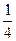 .
.
Однако, область D может быть и не прямоугольной. Аналогично тому, как массив в программировании может быть не прямоугольным, тогда во внутреннем цикле двойного цикла границы переменные и зависят от переменной, определённой во внешнем цикле:
for i : = 1 to 10 do
for j : = 1 to i do
read (a[i,j]);
end;
end;
В случае, если область не прямоугольная, границы вложенного интеграла могут быть не числами, а зависеть от внешней переменной. Рассмотрим пример.
Пример.Вычислить 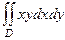 , D - треугольник с вершинами (0,0), (1,0), (1,1).
, D - треугольник с вершинами (0,0), (1,0), (1,1).
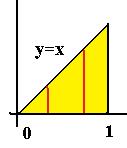
Решение.Границы фигуры по переменной 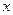 это
это 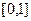 , при других значениях
, при других значениях 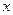 нет точек этого треугольника вообще. При каждом
нет точек этого треугольника вообще. При каждом 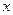 , вертикальный отрезок имеет разную высоту, сначала вообще 0, а затем чем правее, тем больше. Чем больше
, вертикальный отрезок имеет разную высоту, сначала вообще 0, а затем чем правее, тем больше. Чем больше 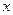 , тем выше отрезок по
, тем выше отрезок по 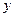 . Вертикальные отрезки внутри треугольника от высоты 0 доходят до линии
. Вертикальные отрезки внутри треугольника от высоты 0 доходят до линии 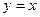 . Поэтому при каждом
. Поэтому при каждом 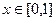 , верно
, верно 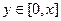 .
.
Интеграл будет записан в виде: 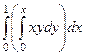 .
.
Граница во внутреннем интеграле зависит от внешней переменной 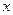 .
.
Границы внешнего интеграла обязательно должны быть контантами.
Во вложенной скобке, вычислится первообразная по 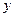 , и будет применена формула Ньютона-Лейбница по
, и будет применена формула Ньютона-Лейбница по 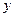 .
.
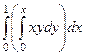 =
= 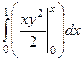 =
= 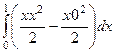 =
= 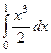 .
.
И хотя границы зависят от 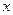 , они подставлены в переменную
, они подставлены в переменную 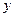 , т.е. всё равно получилась функция от
, т.е. всё равно получилась функция от 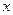 , так же, как если был бы прямоуголник и границы были бы числовыми. Далее, уже обычным путём вычислим интеграл по
, так же, как если был бы прямоуголник и границы были бы числовыми. Далее, уже обычным путём вычислим интеграл по 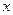 .Итак,
.Итак, 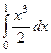 =
= 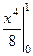 =
= 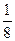 .
.
Дата добавления: 2020-03-17; просмотров: 1001;











