Некоторые свойства криволинейного интеграла.

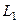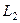1. Если кривая разбита некоторой точкой на две части и , то сумма криволинейных интегралов по двум этим частям равна интегралу по их объединению: .

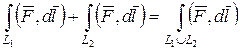Аналог этого свойства был и для определённого интеграла:

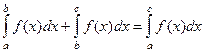
2. Если движение точки по траектории сменить на движение в обратную сторону, то работа силы изменит знак на противоположный: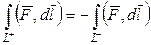

Аналог этого свойства был и для определённого интеграла:

.

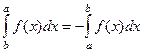Определение. Работа векторного поля по перемещению точки по замкнутойкривой называется циркуляцией.

Обозначение: 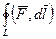или .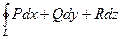

Поверхностные интегралы 2 рода определяются несколько иначе, чем криволинейные. Это связано с тем, что для поверхности, в отличие от кривой, направление касательной в любой точке не единственно: их бесконечно много и они образуют касательную плоскость. Напротив, нормаль соответствует некоторому единственному направлению, перпендикулярному касательной плоскости. Именно по этой причине приняли решение использовать нормаль для построения данных интегралов. Причём нормаль не единичную а такую, чтобы она по длине была равна площади соответствующего участка поверхности. Вспомним определитель, который мы использовали при выводе формулы площади поверхности:

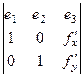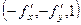= , будем на него скалярно домножать вектор-функцию 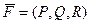. Обозначим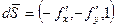

Определение. Пусть дана некоторая поверхность в пространстве 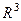. Во всех точках пространства (и в частности, на поверхности) задана ограниченная и непрерывная векторная функция 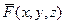. Введём разбиение поверхности на n частей двумя семействами линий, возьмём на каждой из этих частей по одной точке 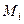. Рассмотрим интегральную сумму: 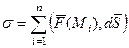. Предел таких сумм при 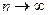называется поверхностным интегралом 2-го рода (от векторной функции).

Обозначается так: .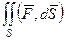

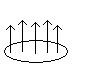
Физический смысл в данном случае не работа силы, а поток векторного поля через поверхность. Чем меньше угол между 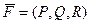и нормалью, тем больше энергии каких-либо лучей проходит через участок поверхности, а к примеру, если 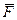направлен по касательной (и перпендикулярен нормали при этом), то лучи скользят вдоль поверхности. Это например, как вблизи полюса лучи солнца почти перпендикулярны нормали к земной поверхности, а вблизи экватора наоборот, близки к нормали.

Чтобы получить формулу вычисления поверхностного интеграла 2 рода, мы должны под интегралом скалярно умножать такие векторы: 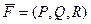и 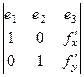= 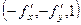. Получаем =

.

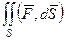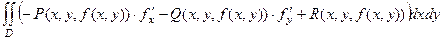Кратко: = .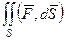

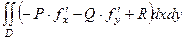Для трёх компонент вектор-функции

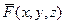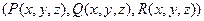= возможно найти 9 различных частных производных, все они записаны в следующей матрице:

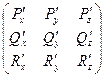
Сумма тех трёх из них, что расположены по гравной диагонали, называется двивергенцией поля.

Определение. Дивергенция векторного поля.

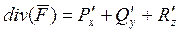(сумма элементов главной диагонали производной матрицы). Это скалярная величина.

Определение.Ротор векторного поля.

= =

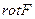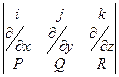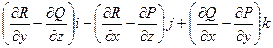
в других обозначениях это выглядит так: .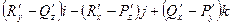

Таким образом, ротор - это некоторое новое векторное поле из 3 компонент, построенное с помощью исходного векторного поля.

Определение. Если ротор = 0 то поле называется безвихревым.

Обратим внимание, что при определении дивергенции используются 3 частных производных, которые расположены в производной матрице по диагонали: дифференцируется i-я компонента по i-й переменной, а при определении ротора - только производные компонент по «чужим» номерам переменных, таких 6 из 9 в производной матрице.