Рассмотрим несколько примеров на тему «полярные координаты».
Пример. Доказать формулу площади круга 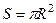 с помощью полярных координат.
с помощью полярных координат.
Решение. Так как надо вычислить площадь, то считаем 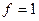 .
.
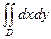 =
= 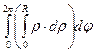 =
= 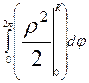 =
= 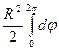 =
= 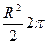 =
= 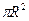 .
.
Пример. Вычислить интеграл 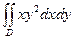 где D - четверть круга единичного радиуса в первой четверти плоскости.
где D - четверть круга единичного радиуса в первой четверти плоскости.
В декартовых координатах, этот интеграл имеет такой вид:
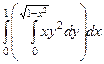 , что при вычислении внутреннего интеграла дало бы
, что при вычислении внутреннего интеграла дало бы 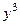 , в итоге привело бы к
, в итоге привело бы к 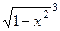 и потребовало бы ещё серию подстановок. В полярных координатах, решение гораздо более просто и удобно.
и потребовало бы ещё серию подстановок. В полярных координатах, решение гораздо более просто и удобно.
Луч находится в 1 четверти при 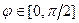 . Радиус 1. Тогда:
. Радиус 1. Тогда:
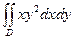 =
= 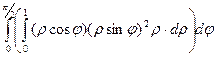 =
= 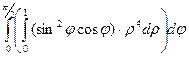 =
= 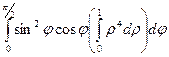 =
=
= 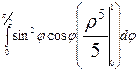 =
= 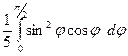 =
=
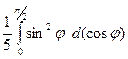 =
= 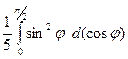 =
= 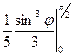 =
= 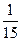 .
.
Кстати, множители, не зависящие от 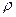 , можно было сразу вынести во внешний интеграл, как видим, они всё равно умножаются на первообразную по
, можно было сразу вынести во внешний интеграл, как видим, они всё равно умножаются на первообразную по 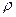 и остаются неизменными, и выносятся во внешний интеграл по
и остаются неизменными, и выносятся во внешний интеграл по 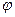 .
.
Пример.Вывести формулу площади сферы 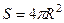 .
.
Решение.
Вспомним формулу S поверхности 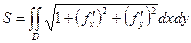 ,
,
рассмотрим верхнюю полусферу, она задана функцией: 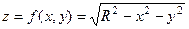 .
.
При этом область определения данной функции - плоская область D - это круг радиуса 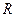 .
.
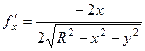 ,
, 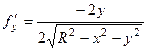 . Тогда
. Тогда
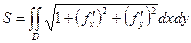 =
= 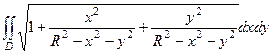
= 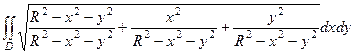 =
=
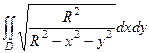 =
= 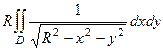 . Теперь переходим к полярным координатам, заодно домножая на определитель Якоби
. Теперь переходим к полярным координатам, заодно домножая на определитель Якоби 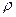 .
.
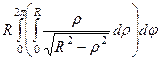 =
= 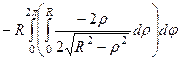
(домножили и поделили на 2, чтобы образовать полный дифференциал подкоренного выражения 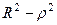 ) .
) .
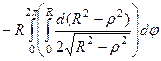 =
= 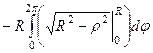 =
= 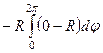 =
=
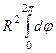 =
= 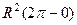 =
= 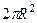 . Напомним, что это площадь верхней полусферы. Соответственно, площадь всей сферы в 2 раза больше, и равна
. Напомним, что это площадь верхней полусферы. Соответственно, площадь всей сферы в 2 раза больше, и равна 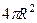 .
.
Дата добавления: 2020-03-17; просмотров: 841;











