Множества с односвязной границей.
1. Множество, такое, что любую пару его точек можно соединить линией, состоящей из точек этого же множества, называется односвязным. Так, например, круг или квадрат - односвязные множества, а два круга, разделённые некоторым расстоянием - нет.
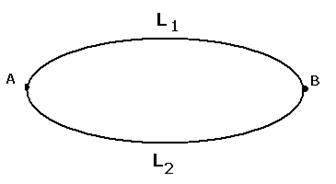
2. Если существуют какие-то внутренние области, не принадлёжащие множеству, то его гарница не будет односвязной. Например, кольцо как плоское множество является односвязным, любую пару точек можно соединить какой-либо кривой. Но его граница не является односвязной, а состоит из двух окружностей, и не всякую пару точек на границе можно соединить кривой, лежащей на границе. Например, если А,В на внешней и внутреннней окружности, то соединяющая кривая проходит не только по границе:
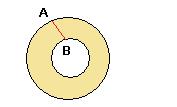
Если граница односвязна, то это означает, что внутри плоской области нет пустот, то есть областей, не принадлежащих данному множеству, тогда каждый замкнутый контур можно стянуть в точку. Такая область - это например, круг, но не кольцо.
Далее мы будем рассматривать многие факты именно для множеств с односвязной границей.
Теорема 1. Криволинейный интеграл 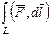 не зависит от пути
не зависит от пути 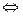 циркуляция по замкнутому контуру
циркуляция по замкнутому контуру 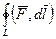 равна 0.
равна 0.
Доказательство.
Необходимость. Пусть интеграл зависит только от начальной и конечной точки, и не зависит от пути, соединяющего точки А,В. А нам надо доказать, что циркуляция по замкнутому контуру равна 0. Возьмём замкнутый контур, разобьём его какими-нибудь случайно взятыми точками. Посколку работа силы не зависит от того, выбран путь 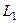 или
или 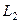 , то:
, то:
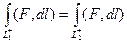
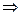
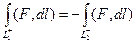
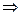
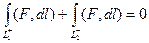 . Но так как объединение 2 частей в замкнутый контур это
. Но так как объединение 2 частей в замкнутый контур это 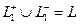 , то получается:
, то получается: 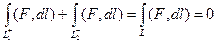 .
.
Достаточность.
Пусть для любого замкнутого контура 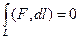 . Если даны какие-то точки А,В, и какие-то две различные линии, соединяющие их, то эти две линии можно объединить в единый замкнутый контур.
. Если даны какие-то точки А,В, и какие-то две различные линии, соединяющие их, то эти две линии можно объединить в единый замкнутый контур.
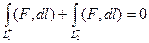
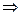
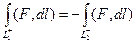
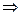
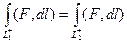 ,
,
что и требовалось доказать.
Давно известна формула Ньютона-Лейбница, выражающая взаимосвязь между интегралом по отрезку и значениями первообразной на его границе (граница состоит из 2 точек). Но подобные взаимосвязи есть также и и между плоской областью и её границей.
Теорема 2. (Формула Грина) Для плоского векторного поля 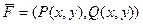 во множестве с односвязной границей верна формула:
во множестве с односвязной границей верна формула: 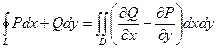 .
.
Доказательство.Спроецируем область на ось Ох, обозначим границы проекции: точки 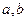 . Сама граница области тогда условно подразделяется на две линии, снизу
. Сама граница области тогда условно подразделяется на две линии, снизу 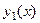 , а сверху
, а сверху 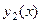 . Чтобы движение по замкнутому контуру происходило против часовой стрелки, надо по
. Чтобы движение по замкнутому контуру происходило против часовой стрелки, надо по 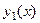 двигаться слева направо, а по
двигаться слева направо, а по 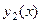 справа налево.
справа налево.
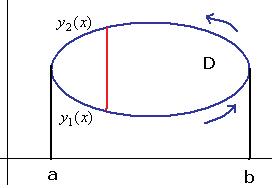
Рассмотрим подробнее интеграл от функции 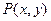 по границе области. В соответствии со всем сказанным, он может быть записан так:
по границе области. В соответствии со всем сказанным, он может быть записан так: 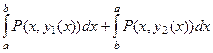 . Но во втором интеграле можно изменить
. Но во втором интеграле можно изменить 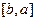 на
на 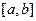 , сменив знак.
, сменив знак.
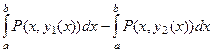 и их можно объединить
и их можно объединить
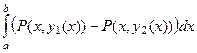 =
= 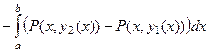
разность, которая внутри интеграла, является результатом применения формулы Ньютона-Лейбница по переменной 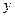 :
:
запишем это в виде: 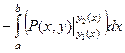 .
.
Но если формула Ньютона-Лейбница применяется к 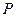 , значит,
, значит, 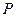 это первообразная по
это первообразная по 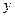 , а она очевидно, является первообразной от своей производной
, а она очевидно, является первообразной от своей производной 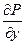 . То есть:
. То есть:
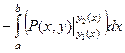 =
= 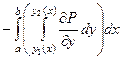 а этой как раз и есть двойной интеграл по области D.
а этой как раз и есть двойной интеграл по области D.
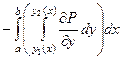 =
= 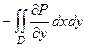 .
.
Аналогично можно спроецировать область D на ось Оу, допустим проекция займёт некоторый отрезок 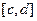 . Левую и правую линии, составляющие замкнутый контур, обозначим
. Левую и правую линии, составляющие замкнутый контур, обозначим 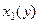 и
и 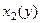 . Правая здесь будет
. Правая здесь будет 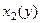 (она дальше от оси Оу).
(она дальше от оси Оу).
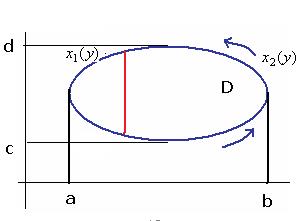
Тогда 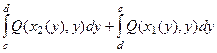 =
= 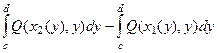 =
= 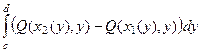 =
=
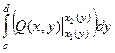 =
= 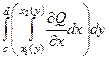 =
= 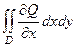 .
.
Сложим два полученных равенства и получается двойной интеграл
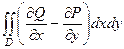 .
.
Что и требовалось докащать.
Другими словами, формула Грина устанавливает следующий факт: циркуляция поля по границе области равна двойному интегралу от функции 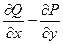 по плоской области. Есть и более общая формула, для 3-мерноно случая.
по плоской области. Есть и более общая формула, для 3-мерноно случая.
Пусть L - замкнутая пространственная кривая, S - поверхность, натянутая на эту кривую, т.е. кривая является краем поверхности, для наглядности представьте например, окружность и полусферу, то есть, S не обязано лежать в плоскости. Циркуляция по контуру L выражается через поверхностный интеграл по S, а именно, равна потоку ротора через S. Эта взаимосвязь выражена в формуле Стокса, которая является обобщением формулы Грина на пространственный случай.
Формула Стокса. 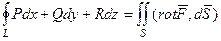 .
.
В формуле Грина, в отличие от формулы Стокса, была использована лишь одна из трёх координат ротора, для плоского поля только 3-я координата отлична от 0.
Пример вычисления работы поля 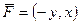 по единичной окружности без формулы Грина и по формуле Грина.
по единичной окружности без формулы Грина и по формуле Грина.
Способ 1. Параметрически: 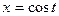 ,
, 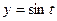 ,
, 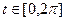 .
.
При этом 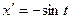 ,
, 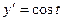 .
.
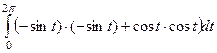 =
= 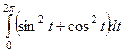 =
= 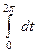 =
= 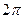 .
.
Способ 2. 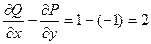 . Тогда
. Тогда 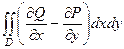 =
= 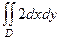 =
= 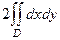 где D - круг радиуса 1. Тогда интеграл от 1 это его площадь.
где D - круг радиуса 1. Тогда интеграл от 1 это его площадь. 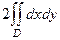 =
= 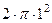 =
= 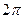 .
.
Дата добавления: 2020-03-17; просмотров: 1449;











