ЗАКОНЫ КОНОВАЛОВА. АЗЕОТРОПНЫЕ СМЕСИ.

Соотношения между составами равновесных растворов и их паров, а также общим давлением пара над раствором были установлены Д.П. Коноваловым в 1881 году и носят название законов Коновалова.

Первый закон Коновалова гласит: общее давление пара над раствором растёт с ростом доли в растворе того компонента, который богаче представлен в паре, т. е. более легколетучего компонента. На этом явлении основана фракционная перегонка (ректификация), позволяющая разделить смесь взаимно–растворимых жидкостей.

Второй закон Коновалова касается более частных случаев. Для некоторых реальных растворов с большими отклонениями от закона Рауля на кривых «общее давление пара – состав» могут появляться минимумы или максимумы.

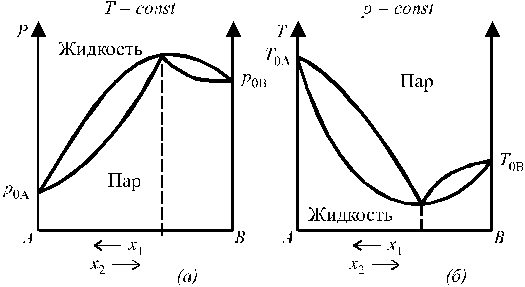
Второй законКоновалова гласит: максимум на кривой общего давления соответствует минимуму на кривой температур кипения и отвечает такому равновесию раствора и его насыщенного пара, при котором составы фаз одинаковы, и наоборот. Диаграммы состояния бинарных систем с максимумом на кривой давления пара и минимумом на кривой температур кипения представлены на рис. 10.

Смеси, у которых раствор и пар одинаковы по составу, называются азеотропными, или нераздельнокипящими. Путём перегонки азеотропные растворы не разделяются (составы фаз равны). Но их можно разделить следующими методами:

— путём химического связывания одного из компонентов;

— путем добавления в систему третьего компонента;

— путем ректификации на двух последовательных колонках при различных давлениях.

Рис. 10. Диаграммы состояния бинарных систем с максимумом

на кривой давления пара (а) и минимумом на кривой температур кипения (б).

Примерами азеотропных смесей с минимумами на кривых температур кипения являются растворы, содержащие Н₂О и С₂Н₅ОН (96,5%), метанол и ацетон, и другие. Примерами азеотропных смесей с максимамуми на кривых кипения являются растворы, содержащие Н₂О и НСl (20%), ацетон и хлороформ, и другие.

Ограниченная взаимная растворимость жидкостей.