Полярная система координат на плоскости.

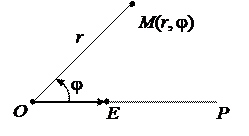Выберем на плоскости произвольные точку O и ось OP, которая задается единичным направленным отрезком . Пусть M – произвольная точка плоскости. Обозначим r = OM, j = Ð(, ) – ориентированный угол. Тогда пара (r, j) называется полярными координатами точки M.

Точка O называется полюсом, а OP – полярной осью. Совокупность точки O и оси OP называется полярной системой координат на плоскости.

Очевидно, что 0£ r < +¥ , а для угла j обычно договариваются, что 0£ j < 2p, либо, что – p< j £ p. При этом, если r = 0, то считается j неопределенным.

Найдем связь между декартовыми и полярными координатами точки M. Выберем декартову СК так, чтобы точка O была ее началом, а положительное направление оси Ox совпадало с направлением оси OP. Пусть M₁ и M₂ – проекции точки M на координатные оси Ox и Oy соответственно. Тогда из DOMM₁ и DOMM₂ получаем

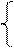
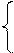x = r cos j , r = ,

y= r sin j.(14) j = arctg . (14¢)

Но последнее равенство верно только для нашего чертежа, когда x > 0. Вообще, знание синуса, косинуса, или тангенса в отдельности не позволяет однозначно определить угол j. Его следует находить сразу из двух равенств:

cos j = x/r, sin j = y/r,

либо так: j = arccos ,если y ³ 0; j = – arccos ,если y < 0 (предполагается, что – p< j £ p). Использование арктангенса неудобно: надо оговаривать еще случай x = 0 и поэтому приходится писать 4 равенства.