Двойное векторное произведение.

Определение. Двойным векторным трех векторов , , называется вектор (´ )´.

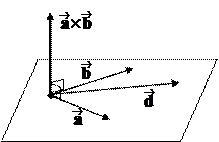Обозначим = (´ )´ . Если ½½ , то ´ = Þ = . Пусть теперь и неколлинеарны. Согласно определению, векторное произведение перпендикулярно сомножителям

Поэтому ^ ´, ^ ´, ^ ´ .

Значит вектор компланарен и . и мы можем разложить через и :

= l + m. (*)

(это верно и в случае = ). Вычислим коэффициенты этого разложения. По определению векторного произведения ^ Û · = 0. Домножим обе части равенства (*) скалярно на вектор :

0 = l( · ) + m( · ).

Очевидно, что уравнение lx + my = 0 относительно неизвестных l и m имеет общее решение (– ky, kx), kÎR. Таким образом

( ´ )´ = – k( · ) + k( · ).

Для того, чтобы вычислить неизвестный координат k, мы вычислим обе части равенства в специально выбранной декартовой СК. Направим ось Ox­­ , а Oy так, чтобы был параллелен плоскости Oxy. Тогда (a₁, 0, 0), (b₁, b₂, 0), (c₁, c₂, c₃). Находим:

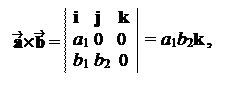
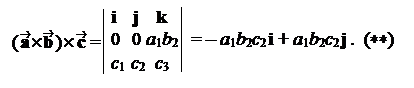
· = a₁c₁, · = b₁c₁ + b₂c₂ ,

( · )= (b₁c₁ + b₂c₂)a₁i, ( · ) = a₁c₁(b₁i + b₂j).

– k( · ) + k( · ) = k(– a₁b₂c₂ i + a₁b₂c₂ j).

Сравнивая последнее равенство с (**) получаем k =1. Итак,

(´)´ = – ( · ) + ( · ) Þ

´( ´ ) = – ( ´ )´ = ( · ) – ( · ) . (23)

Именно в таком виде формулу для вычисления двойного векторного произведения и запоминают. Для этого есть у нее название «бац минус цаб».

Упражнение.Самостоятельно проверьте с помощью этой формулы тождество Якоби:

(´ )´ + ( ´ )´ + ( ´ )´ º .