Сферическая и цилиндрическая системы координат в пространстве.

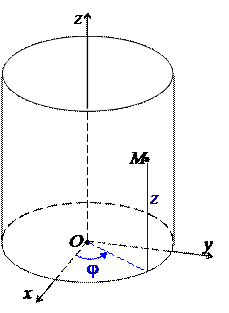
Пусть в пространстве задана декартова СК Oxyz и пусть M(x, y, z) – произвольная точка. Опустим перпендикуляр MM_o на плоскость Oxy. Тогда, очевидно, ½MM_o½= z. Обозначим r =½OM½, y =Ð M_oOM ; при этом, если z >0, то считаем, что y >0, а если z <0, то y <0. Пусть (r, j) – полярные координаты точки M_o на

плоскости. Тогда тройка (r, j, y) называется сферическими координатами точки M, а тройка (r, j, z) – ее цилиндрическими координатами. Очевидно, что 0 £ r < +¥, –p/2 £ y £ p/2 . Если y = ± p/2, то точка M лежит на оси Oz, M_o= O и тогда j считается неопределенным.

Найдем формулы, которые связывают декартовы, сферичес-кие и цилиндрические координаты

точки M. Из DOMM_o находим, что

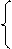
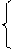r = r×cosy , r = ,

z = r×siny . (15) y = arcsin (15¢)

Эти формулы можно рассматривать, как переход от сферических координат к цилиндрическим и обратно; а j у этих систем координат общее. Формулы (14) и (14¢ ) можно рассматривать, как переход от цилиндрических координат к декартовым, и обратно. Подставляя (15) в (14) получаем формулы перехода от сферических координат к декартовым, а подставляя (14¢ ) в (15¢) получаем формулы перехода от декартовых координат к сферическим:

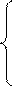
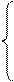x = r cos j×cosy , r = ,

y = r sin j×cosy , (16) j = ± arccos , (16¢)

z = r×siny . y = arcsin( z /r) .

Во второй формуле из (16¢) знак выбирается в соответствии со знаком y.

Сферические координаты можно использовать для введения внутренних координат на сфере. Если начало координат поместить в центр сферы радиуса r, то j и y будут играть роль географических долготы и широты точки M, лежащей на сфере; пишем M(j, y). Точно также цилиндрические координаты позволяют ввести внутренние координаты на поверхности цилиндра. Если начало координат разместить на оси цилиндра радиуса r, то j и z будут координатами точки M, лежащей на поверхности цилиндра; пишем M(j, z).

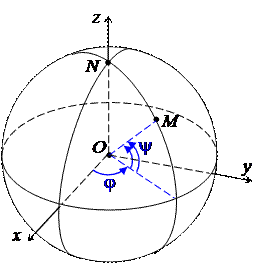Ни в коем случае не следует путать сферические и цилиндрические координаты в пространстве с внутренними координатами на сфере и цилиндрической поверхности. Очень распространена на экзамене ошибка, когда вместо первого рисунка в этом параграфе рисуют второй и третий.