Смешанное произведение векторов.

Определение. Смешанным произведением трех векторов , , называется число (´ ) ·. Оно обозначается · ·, или (, , ).

Теорема 6. Модуль смешанного произведения трех векторов , , численно равен объему параллелепипеда построенного на направленных отрезках , , , представляющих эти векторы, отложенные из одной точки.

Доказательство. Пусть h – высота, опущенная из точки С на основание, которым служит параллелограмм, построенный на направленных отрезках и . Пусть a – угол между h и стороной OC. Тогда

h =½OC½cos a , S_осн =½ ´½.

Пусть b =Ð( ´, ).

1случай. Тройка (, , )

правая. Тогда b = a . Поэтому

V = S_осн · h = ½ ´½½OC½cos a =

=½ ´½½½ cos Ð( ´, ) =

= ( ´ ) · .

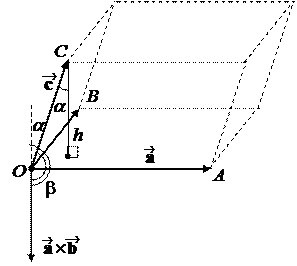2случай. Тройка (, , ) левая. Тогда b = p – a и

cos a = – cos b Þ

V =½ ´½½OC½cos a =

= –½ ´½½½cos Ð( ´, ) =

=–( ´ ) ·.

Но объем всегда неотрицателен. Поэтому в этом случае ( ´ ) · £ 0, и мы имеем

V =½( ´ ) ·½.

Эта формула подойдет и к первому случаю.

Следствие. 1., , компланарны Û = 0;

2. тройка (, , ) правая Û > 0;

3. тройка (, , ) левая Û < 0.

Действительно, объем параллелепипеда равен нулю Û векторы , , компланарны. Если же они образуют левую тройку, то мы уже доказали, что £ 0 , а так как они в этом случае некомпланарны, то неравенство будет строгим. Аналогично, если тройка (, , ) правая, то ³ 0 и , , некомпланарны; поэтому неравенство будет строгим.

Свойства смешанного произведения.

1. Смешанное произведение не зависит от группировки сомножителей: ( ´ ) · = · ( ´ );

2.Смешанное произведение не изменяется при циклической перестановке сомножителей: = = .

3. При перестановке любых двух сомножителей смешанное произведение меняет знак: = – = – = – .

4. (l) = (l ) = (l ) = l( ).

5. ( + ) = + .

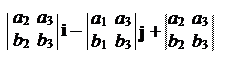Доказательство. 1. Используя свойства определителя получаем

(´ ) · = ( k) ×(c₁i + c₂j + c₃k) =

·(´ ) .

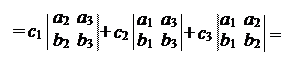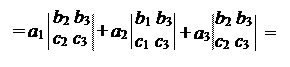
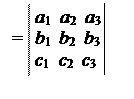
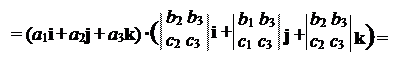
Именно это свойство позволяет использовать обозначение без расстановки скобок. Попутно мы доказали формулу

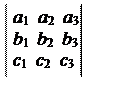= (13)

Все остальные свойства смешанного произведения вытекают из аналогичных свойств определителя.