Общее преобразование координат в пространстве.

Пусть в пространстве заданы две совершенно произвольные аффинные системы координат с общим началом, R = {O, , , } и R ¢ = {O, , , } – реперы, с помощью которых они определяются. Пусть – произвольный вектор, (x₁, x₂, x₃) – его координаты в первой СК, (, x₂¢ , x₃¢ ) – во второй. Будем называть (x₁, x₂, x₃) старыми координатами вектора , а (, x₂¢ , x₃¢ ) – новыми его координатами.

Найдем связь между этими координатами. Пусть нам известно разложение базисных векторов второго базиса B ¢ = { , , } по первому базису B = { , , } :

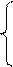= с₁₁ + с₂₁ + с₃₁ ,

= с₁₂ + с₂₂ + с₃₂ , (20)

= с₁₃ + с₂₃ + с₃₃ .

Составим из коэффициентов этого разложения матрицу, выписывая коэффициенты разложения из каждой строки в столбец с тем же номером:

с₁₁ с₁₂ с₁₃

С = с₂₁ с₂₂ с₂₃

с₃₁ с₃₂ с₃₃ .

Эта матрица называется матрицей перехода от первого базиса ко второму. Имеем:

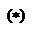= x₁ + x₂ + x₃

= x₁¢ + x₂¢ + x₃¢ .

Подставим в последнее равенство выражения (20):

= x₁¢ (с₁₁ + с₂₁ + с₃₁) + x₂¢ (с₁₂ + с₂₂ + с₃₂ ) + x₃¢ (с₁₃ + с₂₃ + с₃₃ ).

Раскроем скобки и сгруппируем коэффициенты при одинаковых векторах:

= (с₁₁x₁¢ + с₁₂x₂¢ + с₁₃x₃¢ ) + (с₂₁+ с₂₂x₂¢ + с₂₃x₃¢ ) + (с₃₁+ с₃₂x₂¢ + с₃₃x₃¢ ) .

Сравниваем с (*), и в силу единственности разложения вектора по базису, получаем

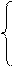x₁= с₁₁x₁¢ + с₁₂ x₂¢ + с₁₃ x₃¢ ,

x₂ = с₂₁+ с₂₂ x₂¢ + с₂₃x₃¢ , (21)

x₃ = с₃₁+ с₃₂x₂¢ + с₃₃ x₃¢ .

Если использовать столбцы, составленные из координат

x₁ x₁¢

X = x₂ X ¢= x₂¢

x₃ , x₃¢ ,

То систему (21) можно переписать в виде одного матричного равенства:

X = CX ¢ (21¢ )

Þ X ¢= C ^–1X ,(22)

т.е. для того, чтобы найти новые координаты вектора по старым, необходимо выписать формулы, аналогичные (21), только в качестве коэффициентов будут использованы элементы матрицы C ^–1, а штрихи у координат будут стоять в левых частях равенств. Можно решить систему уравнений (21) относительно неизвестных x₁¢ , x₂¢ , x₃¢ и мы получим те же формулы.

К сожалению, не всегда к моменту изучения этого параграфа студенты успевают пройти по алгебре произведение матриц и обратную матрицу. Но ко времени экзамена этот материал обязательно должен быть пройден. Необходимые пояснения будут даны на практических занятиях по геометрии.

Координаты точки совпадают с координатами ее радиус-вектора, поэтому они пересчитываются по тем же формулам (21¢) и (22). Заметим, что все рассуждения, приведенные при выводе формул (17) и (17¢) верны и для произвольной аффинной СК. Поэтому в случае переноса начала координат в точку O¢(a, b, c) координаты точки пересчитываютcя по формулам

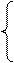
x₁= x₁¢ + a, x₁¢ = x₁ – a,

x₂ = x₂¢ + b, (22) x₂¢ = x₂ – b, (22¢)

x₃ = x₃¢ + c. x₃¢ = x₃ – c.

Все сказанное выше верно и для преобразования аффинной СК на плоскости.