Преобразование координат.

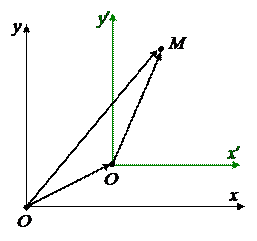
Пусть на плоскости заданы две декартовы системы координат Oxy и O¢x¢y¢, у которых направления координатных осей совпадают, но начальные точки O и O¢ разные. Говорим, что вторая СК получена из первой переносом начала координат в точку O¢.

Пусть нам известны координаты точки O¢ относительно первой СК: O¢(a, b). Пусть M – произвольная точка на плоскости, (x, y) – ее координаты относительно первой СК, (x¢, y¢) – относительно второй СК. Найдем связь между этими координатами.

По определению, координаты точки совпадают с координатами ее радиус-вектора. Поэтому

(a, b), (x, y), (x¢, y¢).

По правилу треугольника сложения векторов

= + .

Отсюда

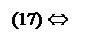
x = x¢ + a, x¢ = x – a,

y = y¢ + b. y¢= y – b.

Аналогично, если в пространстве мы совершим перенос начала координат в точку O¢(a, b, c), то к

формулам (17) и (17¢ ) только добавятся равенства z¢= z + c и z = z¢+ c .

Заметим, что все наши рассуждения справедливы и в случае переноса начала произвольной аффинной СК.

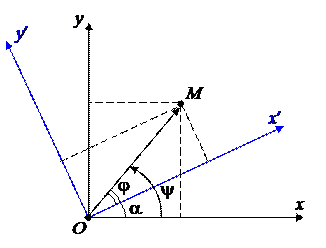Пусть теперь на плоскости заданы две декартовы СК с общим началом: Oxy и Ox¢y¢. Пусть a – ориентированный угол между положительными направлениями осей Ox и Ox¢. Тогда говорим, что вторая СК получена из первой поворотом на угол a. Пусть M – произвольная точка на плоскости, (x, y) – ее координаты относи-

тельно первой СК, ( x¢, y¢) – относительно второй СК.

Найдем связь между этими координатами. Пусть j – ориентированный угол между положительным направлением оси Ox и вектором , а y – между Ox¢ и . Тогда j = y + a . Обозначим r =½OM½. Тогда

x = r cos j , x¢= r cos y,

y = r sin j . y¢= r sin y .

x = r cos (y + a) = r cos y ×cos a – r sin y×sin a = x¢×cos a – y¢×sin a,

y = r sin (y + a) = r cos y ×sin a + r sin y×cos a = y¢×sin a + y¢×cos a.

Итак,

x = x¢×cos a – y¢×sin a,

y = x¢×sin a + y¢×cos a.

Поскольку вторая СК может быть получена из первой поворотом на угол – a, то с учетом cos(-a) = cos a, sin(-a) = – sin a , из (18) получаем

x¢= x ×cos a + y×sin a,

y¢= – x ×sin a + y×cos a.

Если в пространстве совер-шается поворот СК вокруг оси Oz, то координата z точки M не изменится, а x и y будут изменяться по тем же формулам (18) и (18¢). Самостоятельно выпишите формулы преобразования координат при повороте СК в пространстве вокруг Ox и Oy.

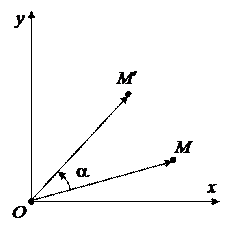Важно не путать поворот СК с поворотом плоскости. Пусть точ-ка M ¢(x¢, y¢) получается из точки M(x, y) поворотом вокруг начала координат на угол a . Для того, чтобы найти, как выражаются (x¢, y¢) через (x, y) мы представим ситуацию так: точка M остается на месте, а СК поворачивается в обратном направлении, т.е. на угол – a . Поэтому имеем формулы

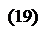x¢= x×cos a – y×sin a,

y¢= y×sin a + y×cos a.

Допустим, теперь на плоскости заданы две совершенно произвольные декартовы СК Oxy и O¢x¢y¢. Тогда вторую СК можно получить из первой в результате двух преобразований: сначала мы совершаем перенос начала координат в точку O¢ (получим промежуточную СК O¢x²y²), а затем – поворот координатных осей. Тогда

x²= x – a, x = x²+ a,

y²= y – b. y = y²+ b.

x¢ = x²×cos a + y²×sin a, x²= x¢×cos a – y¢×sin a,

y¢ = –x²×sin a + y²×cos a. y²= y¢×sin a + y¢×cos a.

Подставляя x² и y² из первой системы в третью, получаем, что

x¢= (x – a)×cos a + (y – b)×sin a,

y¢= –(x – a)×sin a + (y – b)×cos a.

Упражнение. Самостоятельно выпишите формулы, по которым (x, y) выражаются через (x¢, y¢ ).