Первообразная. Неопределенный интеграл

Пусть функция f(x) есть производная от функции F(x), т.е. F¢(x) = f(x). Тогда функция F(x) называется первообразной для функции f(x).

! Примеры: f(x) = 2x; F(x) = x²; F(x) = x² + 2.

Любая непрерывная функция f(x) имеет бесконечное множество первообразных; если F(x) первообразная, то F(x) + C тоже первообразная, где C - неопределенный коэффициент.

Наиболее общий вид первообразной от функции f(x) называется неопределенным интегралом:

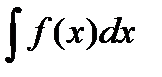= F(x) + C.

Слово интеграл заимствован от латинского слова integralis – целостное. Процедура нахождения первообразной F(x) называется интегрированием, f(x)dx - подинтегральное выражение, f(x) - подинтегральная функция, x - переменная интегрирования, 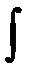- знак интеграла..

! Примеры: ; .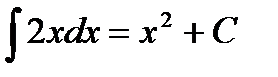

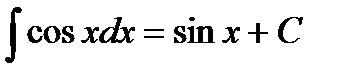Свойства неопределенных интегралов

1. Дифференцирование и интегрирование – это обратные действия. Они взаимно уничтожают друг друга: 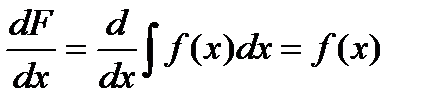или .

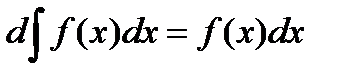2. Постоянный множитель можно вынести за знак интеграла: .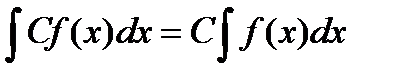

3. Интеграл суммы равен сумме интегралов:

.

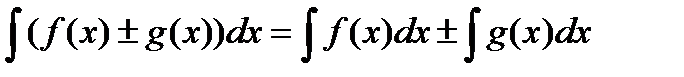ТАБЛИЧНЫЕ ИНТЕГРАЛЫ. ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ