Свойства степенных рядов
1. Сумма S(x) степенного ряда является непрерывной функцией в интервале сходимости (– R; R).
2. Степенные ряды 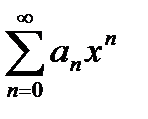 и
и 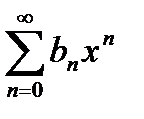 , имеющие радиусы сходимости соответственно R1 и R2, можно почленно складывать, вычитать и умножать. Радиус сходимости произведения, суммы и разности рядов не меньше, чем меньшее из чисел R1 и R2.
, имеющие радиусы сходимости соответственно R1 и R2, можно почленно складывать, вычитать и умножать. Радиус сходимости произведения, суммы и разности рядов не меньше, чем меньшее из чисел R1 и R2.
3. Степенной ряд внутри интервала сходимости можно почленно дифференцировать:
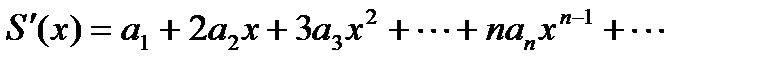
Полученный степенной ряд имеет тот же радиус сходимости, что и исходный степенной ряд.
4. Степенной ряд можно почленно интегрировать на каждом отрезке внутри интервала сходимости:
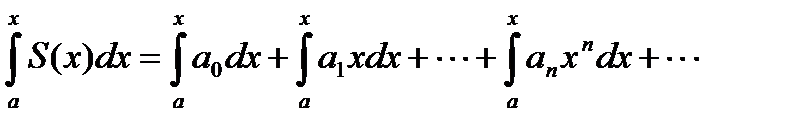
Полученный степенной ряд имеет тот же радиус сходимости, что и исходный степенной ряд.
Ряд Тейлора
Функцию f(x) можно представить в виде бесконечного степенного ряда, который называется рядом Тейлора:
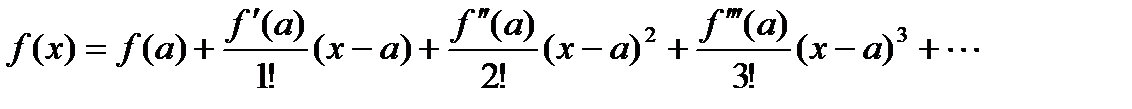
Частный случай этого ряда при a = 0 называется рядом Маклорена:
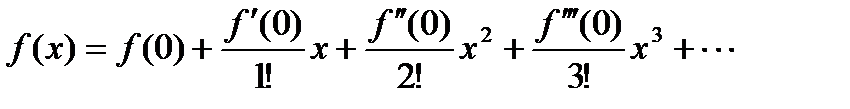
! Примеры: 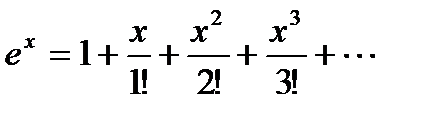 ,
,
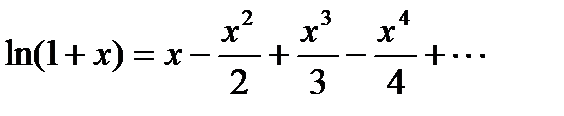
Значение функции в точке x = b можно приближенно найти с помощью ограниченного ряда Тейлора (с помощью первых n членов) (формула Тейлора):
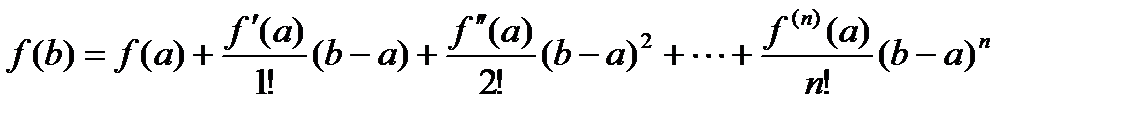 (1),
(1),
допустив при этом ошибку (остаточный член Лагранжа):
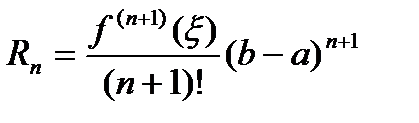 , (2)
, (2)
где x - некоторое число, лежащее между a и b.
Коши доказал, что f(x) разлагается в ряд Тейлора, если 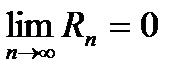 .
.
@ Задача 3. Найти формулы для вычисления чисел e, 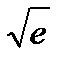 и функции
и функции 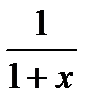 .
.
Решение: e и 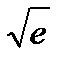 находятся с помощью формулы (1) и остаточного члена (2):
находятся с помощью формулы (1) и остаточного члена (2):
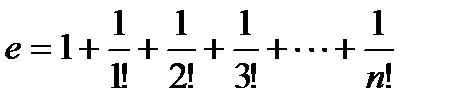 ,
, 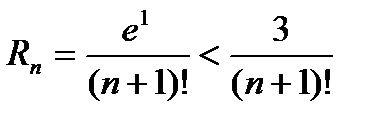 ,
,
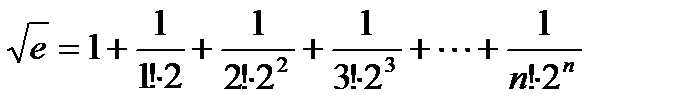 ,
, 
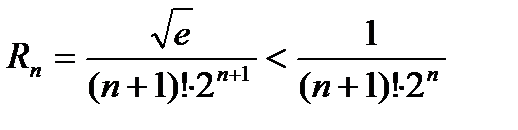 .
.
Функция 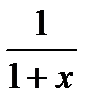 находится с помощью выражения для f(x) (формула (1), только вместо b нужно подставить x) и остаточного члена (2):
находится с помощью выражения для f(x) (формула (1), только вместо b нужно подставить x) и остаточного члена (2):
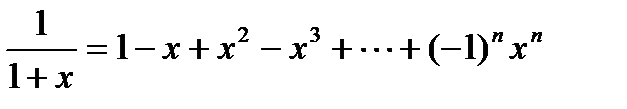 ,
, 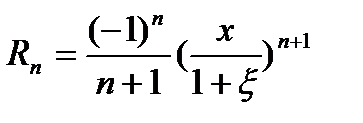 .
.
Дата добавления: 2016-06-15; просмотров: 5809;











