Предел и непрерывность функции

При нарушении хотя бы одного из этих условий функция называется разрывной в точке x = a.

Точка x = a называется точкой разрыва первого рода функции y = f(x), если в этой точке существуют конечные пределы функции слева (b₁) и справа (b₂) (односторонние пределы). Величину |b₁ – b₂| называют скачком функции.

Разрывная функция с точкой устранимого разрыва может стать непрерывной функцией, путем добавления значения f(x) = b в точке разрыва x = a. В приведенном примере – это значение f(0) = 1.

При b₁ ≠ b₂, точка x = a называется точкой конечного разрыва

Пример: 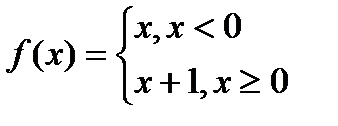, |b₁ – b₂| = 1.

При b₁ = b₂, точка x = a называется точкой устранимого разрыва

Пример: 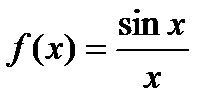, |b₁ – b₂| = |1 – 1| = 0.

Точка разрыва называется точкой разрыва второго рода функции y = f(x), если, по крайней мере, один из односторонних пределов (слева или справа) не существует или равен бесконечности.

@ Задача 1. Найти точку разрыва функции 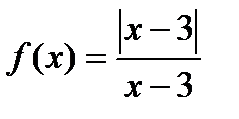. Выяснить род разрыва.

Решение: x = 3 является точкой разрыва функции (функция не определена в этой точке). Левосторонний предел равен b₁ = – 1, а правосторонний предел - b₂ = 1, т.е. это означает, что мы имеем дело с точкой разрыва первого рода. Скачок равен |b₁ – b₂| = 2.

Учитывая вышесказанное, можно дать следующее определение. Функция непрерывна в точке x = a, если она определена в этой точке и выполняется условие Dy ® 0 приDx ® 0, т.е. бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.

Функция y = cosx непрерывна в произвольной точке x, т.к. Dcosx ® 0 приDx ® 0.

Функция называется непрерывной на замкнутом промежутке, если она непрерывна в каждой точке этого промежутка, включая оба конца.