Тертя ковзання змащених тіл

Як було зазначено раніше (п. 6.1), при рідинному терті безпосередньо­го стикання між двома поверхнями, що рухаються одна відносно іншої, не буває, оскільки між цими поверхнями є проміжний мастильний шар рідини. При відносному русі поверхонь окремі шари рідини зсуваються один віднос­но іншого. Отже, тертя в рідинному шарі зводиться до в'язкого зсуву.

Для зручності технічних розрахунків при вивченні рідинного тертя запроваджують поняття коефіцієнта тертя, але на відміну від коефіцієнта сухого тертя коефіцієнт рідинного тертя f залежить від швидкості 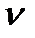руху шарів мастила один відносно одного, навантаження р і коефіцієнта в'язкос­ті 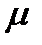, тобто .

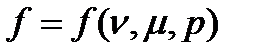Коефіцієнт в'язкості 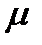називають звичайно абсолютним коефіцієн­том, він характеризує величину опору мастила зсуваючим зусиллям, його одиниця – .

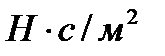Досліджуючи плоскопаралельний рух в'язкої рідини, Ньютон знай­шов, що сила, необхідна для переміщення одного шару рідини паралельно іншому, дорівнює

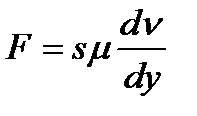, (6.5)

де F є сила в'язкого зсуву; 5 - площа поверхні ковзання; 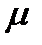- коефіцієнт абсолю­тної в'язкості; 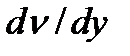- зміна швидкості за висотою шару (градієнт швидкості).

Основоположник гідродинамічної теорії тертя М. П. Петров сформулю­вав основні вимоги, необхідні для заміни сухого тертя рідинним [1], а саме:

1) мастильна рідина, що займає зазор між ковзними поверхнями, повинна затримуватись у зазорах;

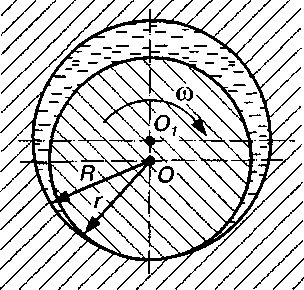
Рис. 6.4. Рідинне тертя в обертовій парі

Для задоволення другої вимоги, необхідно, щоб між ковзними поверхнями безперервно нагніталась мастильна рідина, або щоб між ними був клиновий зазор. Стосовно цапфи, що лежить у підшипнику (рис. 6.4), це досягається тим, що радіуси R підшипника і r цапфи - різні. Завдяки цьому між цапфою і підшипником ство­рюється клиноподібний зазор, у який при обертанні цапфи нагнітається мастильна рідина. При цьому в мастильному шарі виникають сили, що зрівноважують зов­нішнє навантаження на цапфу, і цапфа ні­би „спливає" на шарі мастильної рідини. При цьому з підвищенням кутової швидкості центральна вісь О цапфи намагається збігтися з центральною віссю підшипника .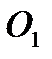

Третя і четверта вимоги відносяться до забезпечення такої об­робки поверхні цапфи і підшипника, за якої зменшилися б можливі нерів­ності і шорсткість на їх поверхнях; крім того, необхідно прагнути до яко­мога менших деформацій цапфи і по можливості старанніше очищати мастильну рідину від сторонніх твердих домішок.

Тертя кочення

Як уже зазначалося, тертям кочення називають опір, який вини­кає при перекочуванні одного тіла по поверхні іншого. Цей опір виникає головним чином від того, що тіла не абсолютно тверді і завжди дещо де­формуються в місцях їх стикання. Досвід показує, що опір перекочуванню тіл залежить від пружних властивостей тіл, які стикаються, їх кривизни та сили притискання.

Фізичні явища, які викликають тертя кочення, так само як і при терті ковзання, вивчені мало; у технічних розрахунках користуються в основно­му даними, одержаними при експериментальних дослідженнях, які проводились над різними конкретними об'єктами: котками, колесами, роликами і шариками в підшипниках кочення тощо.

 

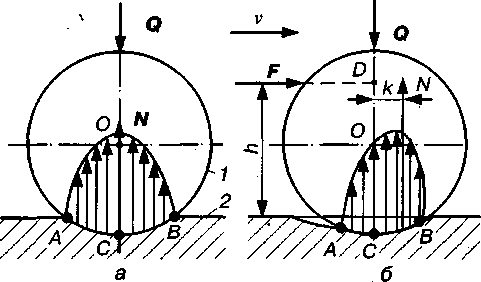
Рис. 6.5. Тертя кочення:

а)коток 1 нерухомий; б) коток 1 рухомий

 

На перемагання опору під час перекочування тіл ви­трачається якась робота, яка в основному йде на дефор­мацію стичних поверхонь. Якщо на нерухомий коток 1, який лежить на горизонта­льній площині 2 (рис. 6.5, а), діє тільки сила 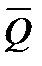, то деформація котка і опорної пове­рхні симетричні відносно лінії дії 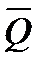. У результаті деформації коток і опорна поверхня дотикаються не в одній точці (лінії), а деякою площинкою контакту, ширина якої АВ. Реакція з боку опорної по­верхні буде розподілена по всій площинці контакту. Згідно з положенням теорії пружності напруження в зоні контакту розподіляються за еліптич­ним законом. При цьому крива напружень симетрична, а значить, напря­мок рівнодіючої 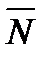цих напружень збігається з напрямком сили 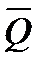. За мо­дулем нормальна реакція 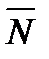дорівнює силі 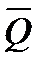і направлена в протилежний від неї бік.

Якщо коток рухається під дією деякої горизонтальної сили 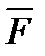(рис. 6.5, б), то деформація котка і опорної поверхні буде вже несимет­рична відносно лінії дії сили 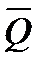(ВС > АС). Це пояснюється тим, що ді­лянка ВС знаходитися у зоні зростання деформації, а ділянка АС – у зоні спадання деформацій. Завдяки внутрішньому тертю в матеріалі тіл, що деформуються, має місце незбіжність кривих навантаження і розвантаження матеріалу (явище пружної післядії і гістерезису). Тому крива напружень у зоні СВ буде вища від кривої в зоні АС, а значить, розподіл напружень відносно лінії дії сили 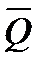буде несиметричним з максимумом, зсунутим у бік руху котка. Отже, рівнодіюча 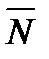напру­жень буде зміщена в бік руху від точки С на величину k, яка називаєть­ся плечем сили, або коефіцієнтом тертя кочення.

Враховуючи, що деформація тіл при коченні незначна порівняно з розмірами тертьових тіл, можна прийняти, що СD = h. Тоді, записавши рівняння моментів сил, що діють на коток, відносно точки С, маємо

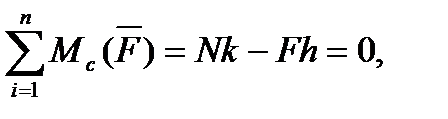
або

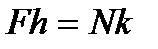(6.6)

Величина 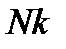називається моментом тертя кочення, а 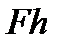- оберталь­ним (рушійним) моментом. Якщо врахувати, що 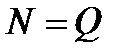, то момент тертя кочення

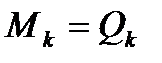(6.7)

де роль коефіцієнта пропорційності відіграє плече тертя k. Як видно з рис. 6.5 і формули (6.7), коефіцієнт тертя кочення k вимірюється одиницею довжини (мм або см) і визначає максимальне значення зміщення нормаль­ної реакції 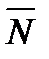відносно лінії дії сили 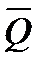. Нагадаємо, що коефіцієнт тертя ковзання f є безрозмірна величина (6.2).

Коефіцієнт тертя кочення залежить від пружних властивостей мате­ріалів тертьових тіл, стану їх поверхні та радіусів кривизни. На практиці, як правило, користуються значеннями, знайденими експериментальним шляхом. Наприклад, для стального колеса і рейки k 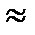0,05мм, для гарто­ваних стальних шариків і роликів - 0,01 мм, чавуну по чавуну - 0,05 мм, дерева по сталі - 0,3-0,4 мм, дерева по дереву - 0,5-0,8 мм.

З рівнянь (6.6) і (6.7) знаходимо силу 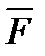, яку необхідно прикласти до котка, щоб він рівномірно перекочувався по площині:

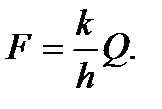(6.8)

На практиці інколи користуються умовною безрозмірною величиною

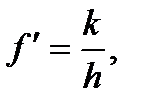(6.9)

яка називається зведеним {умовним) коефіцієнтом тертя кочення. Тоді залежність (6.8) приймає такий же вигляд (6.1), як і при терті ковзання:

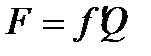. (6.10)

Втрати енергії при терті кочення, як правило, значно менші, ніж при терті ковзання. Ось чому в техніці намагаються якомога більше замінити тертя ковзання тертям кочення. Для цього широко використовується колісний транспорт, підшипники кочення, шарикові або роли­кові напрямні тощо.

Оскільки на практиці звичайно тертя кочення супроводжується тер­тям ковзання, то важливо розглянути, за яких умов яке тертя має місце. Тут можливі три випадки.

 

1. Якщо 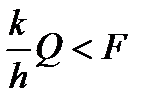, а 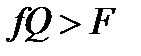, то коток буде тільки котитися, де f – коефіцієнт тертя ковзання. Об'єднавши ці нерівності, одержимо умову чистого кочення

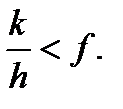(6.11)

Отже, при чистому коченні необхідно, щоб зведений коефіцієнт тер­тя кочення ( 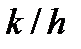) був меншим від коефіцієнта тертя ковзання.

2. Якщо 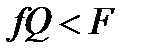, а 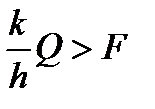, то циліндр буде тільки ковзати. Тоді

умова чистого ковзаннявиражається так:

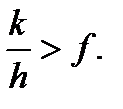(6.12)

При чистому ковзанні необхідно, щоб коефіцієнт тертя ковзання був меншим за зведений коефіцієнт тертя кочення.

3. Якщо ж 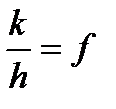, то можливе спільне кочення і ковзання, тобто з'являється невизначеність у русі.

Питання для самоперевірки

1. Що розуміють під силою тертя? Причини виникнення тертя. 2. Чим відрізня­ється тертя кочення від тертя ковзання? Яку роль відіграє мастило, яке знаходиться між тіпами, що мають відносний рух? 3. Від яких факторів залежить сила тертя? 4. Дайте ви­значення коефіцієнта, кута, конуса тертя. Який зв'язок між: коефіцієнтом і кутом тертя?5.Запишіть формулу Амонтона-Кулона, яка дозволяє наближено знайти силу тертя. 6.Чи однакові коефіцієнти тертя спокою і руху? 7. Які вимоги необхідно забезпечити, щоб було рідинне тертя? 8. Що розуміють під коефіцієнтом тертя кочення? 9. Умови чистого кочення і чистого ковзання.

Розділ 9

ЗУБЧАСТІ ПЕРЕДАЧІ

9.1. Загальні відомості про зубчасті передачі

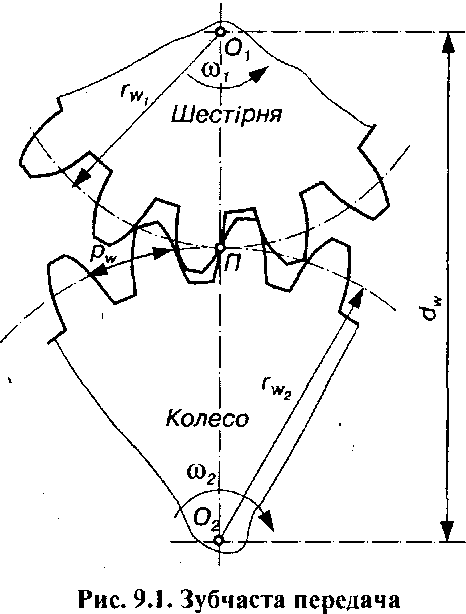
Зубчастою (зубчатою) передачею називають триланковий меха­нізм, в якому два рухомі зубчасті (зубчаті) колеса (або рухоме колесо і рей­ка) утворюють з нерухомою ланкою обертову (або обертову і поступальну) пару, а між собою – вищу пару. У таких механізмах передача руху здійсню­ється механічним зачепленням – зубів вхідного колеса за зуби вихідного ко­леса замість сил. тертя, як це має місце у фрикційних передачах. Обидва ко­леса (рис. 9.1) мають виступи (зуби) і западини такої форми, що зуби одного колеса входять у западини іншого, утворюючи при цьому вищу кінематичну пару. Кожний зуб колеса можна розглядати як окремі кулачки.

Зубчасте колесо передачі з меншим числом зубів (при їх рівності – вхідне зубчасте колесо) називають шестірнею, друге зубчасте колесо передачі – колесом.

У найпростішому випадку зубчасту передачу можна уявити собі як два циліндричні котки (поверхні) з радіусами 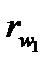і 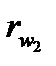, що котяться один по одному без ковзання, маючи точку дотику П. Поверхні, що переко­чуються одна відносно одної без ков­зання, називаються початковими, відповідно'й кола радіусами 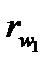і 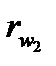називають так само. Точку П дотику цих кіл називають полюсом зубчас­того зачеплення, а лінію, що прохо­дить через точку П паралельно осям обертання коліс і яка є миттєвою віссю відносних швидкостей зубчастих коліс, називають полюсною лінією.

Початкові поверхні зубчастих коліс є аксоїдами у відносному ру­сі (аксоїдами називають поверхні, які описує миттєва вісь відносного руху коліс передачі у системі координат кожного з коліс).

Відстань між осями обертання двох зубчастих коліс, що пере­бувають у зачепленні, називають міжосьовою відстанню. Як видно з рис. 9.1,

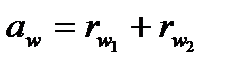. (9.1)

Передаточне відношення зубчастої передачі (відношення кутових швидко­стей зубчастих коліс) виражається так само, як і у фрикційних передачах формулою

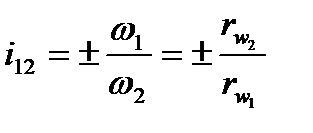. (9.2)

Якщо виразити довжину початкового кола через початковий крок 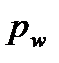, тобто 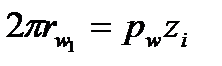, і підставити значення радіусів початкових кіл 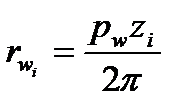у залежність (9.2), то можна записати передаточне відношення через числа зубів коліс:

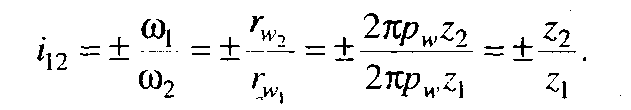
(9.3)

Знак «+» приймають для внутрішнього зачеплення, а «–» – для зовнішнього.

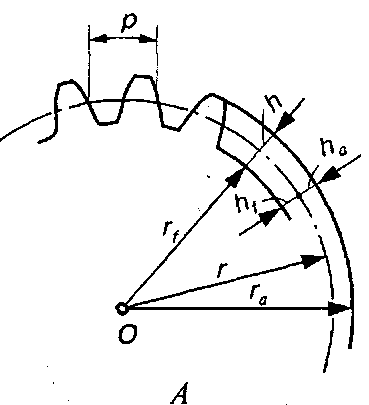
Коловим кроком зубчастого зачеплення р називають відстань між однойменними точками профілів двох сусідніх зубів (рис. 9.1), вимі­ряних по будь-якому колу. Коловий крок

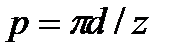, (9.4)

де d – діаметр кола, на якому виміряний крок; z – число зубів колеса.

Значення кроку р залежить від діаметра (радіуса) кола, на яко­му його виміряють, а тому, щоб відрізняти значення кроку на різних колах, вказують нижні індекси, як це, наприклад, виконано для почат­кового кроку .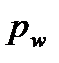

Зубчасті передачі складають найбільш розповсюджену й важливу групу механічних передач. Іх використовують у широкому діапазоні галу­зей і умов роботи: від годинників і приладів – до найважчих машин, для передачі колових сил від міліньютонів до кількох меганьютонів, для моментів до 10⁷ 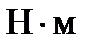і потужностей від безмежно малих до десятків тисяч кіловат, з коловими швидкостями від 2 м/хв до 140 м/с, з діаметрами від частки міліметра до 10 м і більше. Особливо доцільне використання зубча­стих передач, коли необхідно забезпечити стале передаточне відношення або передати великі потужності. Отже, зубчасті передачі порівняно з іншими механічними передачами мають важливі переваги: а) малі габарити; б) високий ККД; в) високу надійність у роботі та простоту в обслуговуванні; г) сталість передаточного відношення через відсутність проковзування; д) можливість використання в широкому діапазоні момен­тів, швидкостей і передаточних відношень.

До недоліків зубчастих передач можна віднести: вимоги високої точності виготовлення, шум при роботі з великими швидкостями обертан­ня коліс і можливість появи вібрацій та ударних навантажень при недос­татній точності виготовлення, неможливість плавного регулювання пере­даточного відношення.

9.2. Типи зубчастих передач

Залежно від розміщення осей валів, між якими здійснюється пере­дача обертового руху, зубчасті передачі поділяються на три типи:

1. Передачі циліндричними зубчастими колесами між паралель­ними валами.

2. Передачі конічними зубчастими колесами між валами, осі яких перетинаються.

3. Передачі гіперболоїдними зубчастими колесами між валами, осі яких схрещуються.

При паралельних осях зубчастих коліс маємо плоский зубчастий механізм. Якщо зуби в циліндричних колесах розміщені паралельно осі колеса, то такі зуби називають прямими, а саме колесо – прямозубим .(рис. 9.2,а). Це найпростіший і найпоширеніший вид зубчастих коліс. Проте їх слід використовувати при малих колових швидкостях коліс ( 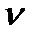<3–6м/с) і не дуже великих навантаженнях. Це пояснюється тим, що зуби в такій передачі входять у контакт відразу по всій своїй довжині, а тому незначні помилки при виготовленні коліс та деформації деталей передачі супрово­джуються шумом, часто призводять до порушення рівномірного лінійного контакту, погіршують плавність роботи передачі. Отже, такі передачі пра­цюють із шумом, мають невисоку плавність роботи і малу несучу здатність.

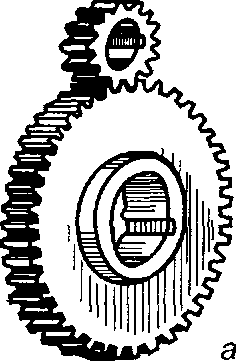
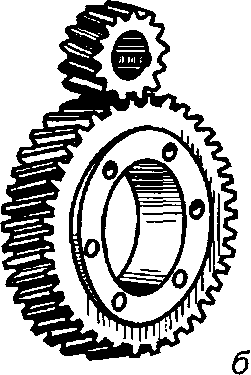
Рис. 9.2. Передачі циліндричними зубчастими колесами між паралельними валами: а) прямозубі; б) косозубі; в) шевронні

При великих колових швидкостях ( 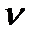>3 м/с) і великих навантаженнях використовують косозубі (тангенці­альні) колеса (рис. 9.2, б), в яких зуби розміщені по гвинтовій лінії, тобто під кутом до твірної початкового циліндра. Передачі з косозубими ко­лесами відрізняються високою плав­ністю зачеплення і меншим шумом при роботі, мають високу несучу здатність. Це пояснюється тим, що зуби входять у зачеплення поступово і в зачепленні одночасно перебуває декілька їх пар. Основним недоліком косозубих передач є наявність осьо­вих сил, які діють як на самі колеса, так і на опори їхніх валів або осей. Як видно з рис. 9.3, а, величина осьової сили 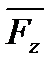залежить від кута нахилу зуба 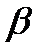( 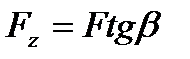, де F – колова сила – складова нормальної сили 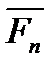, що діє на зуб при передачі руху).

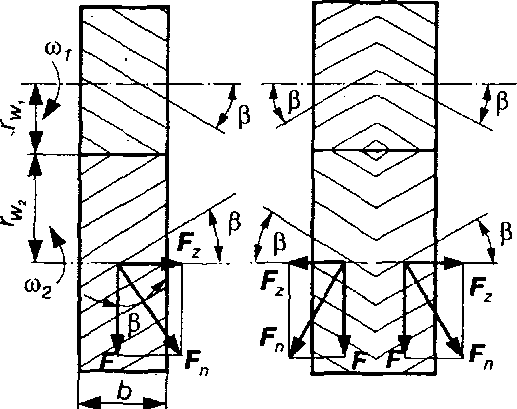
Рис. 9.3. Розподілення сил в зубчастих передачах: а) косозубій; б) шевронній

Внутрішнє та рейкове зачеплення, що показані на рис. 9.4 – це різновиди передач цилінд­ричними зубчастими коле­сами. У першому випадку (рис. 9.4, а) зуби колеса 2 нарізані на внутрішній по­верхні циліндричного тіла, у другому (рис. 9.4, б) – колесо 2 перетворилось у рейку. При цьому рейку можна розглядати як зубчасте колесо діаметром, що прямує до нескінченості. Рейкове зачеплення використовують для перетворення обертового руху в поступальний або навпаки.

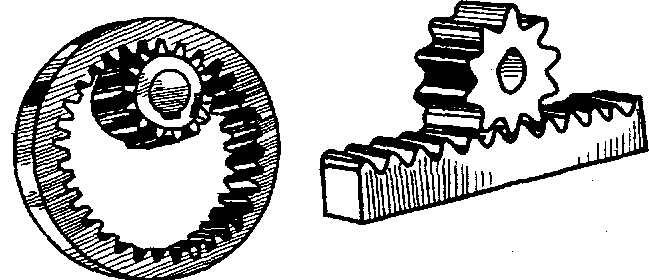
Рис. 9.4. Внутрішнє (а)та рейкове зачеплення (6)

Для передачі обертання між валами, осі яких перетинаються, ви­користовують конічні колеса (рис. 9.5). Найчастіше використовують ко­нічні колеса з кутом перетину між осями валів (міжосьовим кутом) 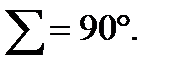Таку передачу називають ортогональною. Якщо поверхні зубців пара­лельні твірним початкових конусів, то такі зубчасті колеса називають прямозубими (рис. 9.5, а). Вони мають усі переваги та недоліки, властиві прямозубим циліндричним зубчастим передачам. Для забезпечення кра­щих умов роботи при великих швидкостях і навантаженнях у конічних ко­лесах доцільно використовувати гвинтові або косі зуби (рис. 9.5, б). Такі передачі працюють більш плавно і безшумно. Шевронні конічні зубчасті колеса не використовують через їх нетехнологічність. На практиці ши­роке розповсюдження одержали конічні колеса з криволінійним зубом (рис. 9.5, в), лінії зуба яких – дуга кола, евольвента, циклоїдні криві. Такі колеса нарізати простіше, ніж косозубі.

Рис. 9.5. Конічні зубчасті передачі:

а) прямозубі; б) косозубі; в) з криволінійним зубом

Для передачі обертання між валами, осі яких схрещуються, можна використовувати гіперболоїдні зубчасті колеса, в основу яких покладені гіперболоїди обертання (рис. 9.6, а), твірні яких – прямі лінії. Якщо уздовж твірних ЕЕ (рис. 9.6, б) нарізати зуби, матимемо гіперболоїдні зубчасті ко­леса, які дозволяють передавати обертовий рух між осями, що схрещують­ся. У зв'язку з тим, що такі зубчасті колеса важко виготовляти, на практиці розповсюджені їх спрощені варіанти, одержані вирізанням різних ділянок гіперболоїдів. Якщо вирізати з гіперболоїда частину його горловини, діс­танемо циліндричні зубчасті колеса 1-2, на віддаленні від горловини – ко­нічні зубчасті колеса 3-4. Такі зубчасті передачі називають - у першому випадку - гелікоїдними або гвинтовими (рис. 9.6, г), у другому – гіпоїд­ними (рис. 9.6, в).

Окремим випадком передач гвинтовими колесами є черв'ячна передача (рис. 9.6, д). На черв'яку 1 кут нахилу зубів дуже великий, тому зуб встигає декілька разів обвити тіло черв'яка; на черв'ячному колесі цей кут відповідно малий, і таке колесо нагадує звичайне косозубе колесо. Черв'як може бути циліндричним (рис. 9.6, д) або глобоїдним (рис. 9.6, е).

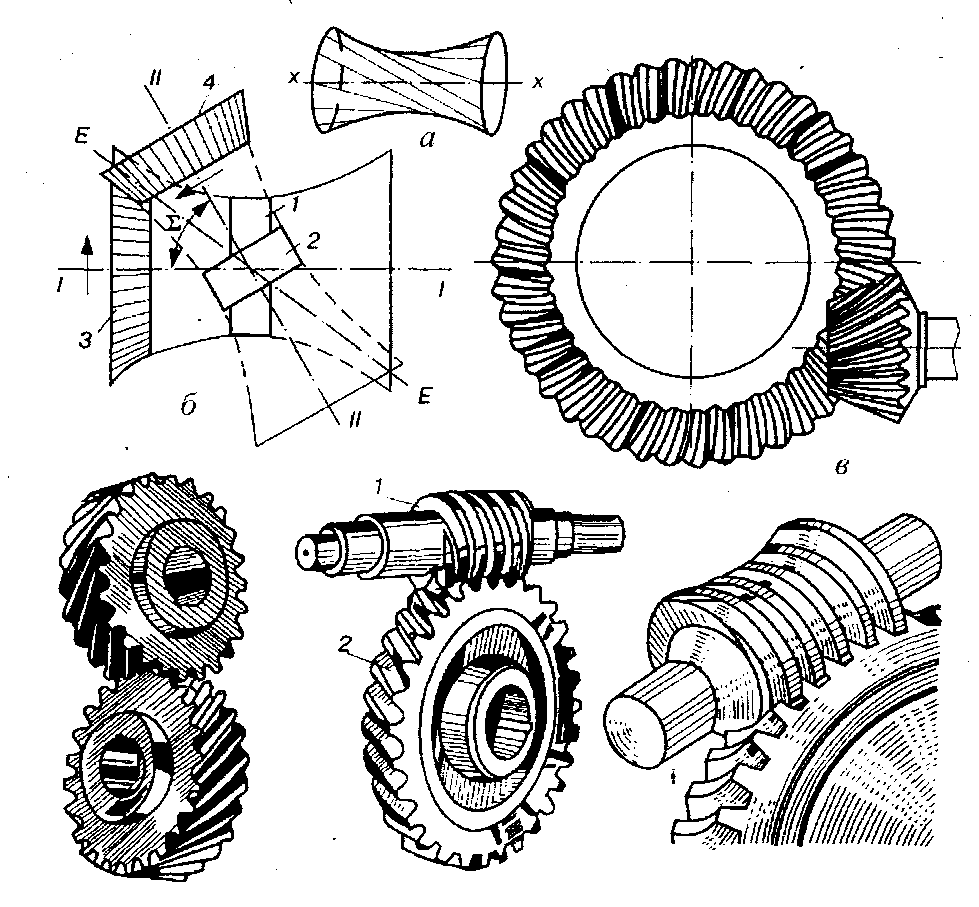
Рис. 9.6. Передачі гіперболоїдними зубчастими колесами:

а) гіперболоїд обертання; б) передача гіперболоїдними зубчастими колесами;

в) гіпоїдна передача; г) гелікоїдна; д) черв'ячна з циліндричним черв'яком; є) черв'ячна з глобоїдним черв'яком

9.3. Геометричні параметри циліндричного зубчастого колеса

Основні параметри зубчастих коліс розглянемо на прикладі ци­ліндричного зубчастого колеса (рис. 9.7, а).

Зубчасте колесо складається з тіла зубчастого колеса 1 і зубчас­того вінця 2. Зубчастий вінець складається із зубів 3 і западин 4. Цилін­дрична поверхня, що відокремлює зуби від тіла зубчастого колеса, нази­вається поверхнею западин 5 (рис. 9.7, б). Поверхня, що обмежує зуби з протилежного від тіла зубчастого колеса боку, називається поверхнею вершин 6. Частина поверхні западин зубчастого колеса, що належить зубу, носить назву основи зуба 7, а частина поверхні вершин, що належить зубу – вершини зуба 8.

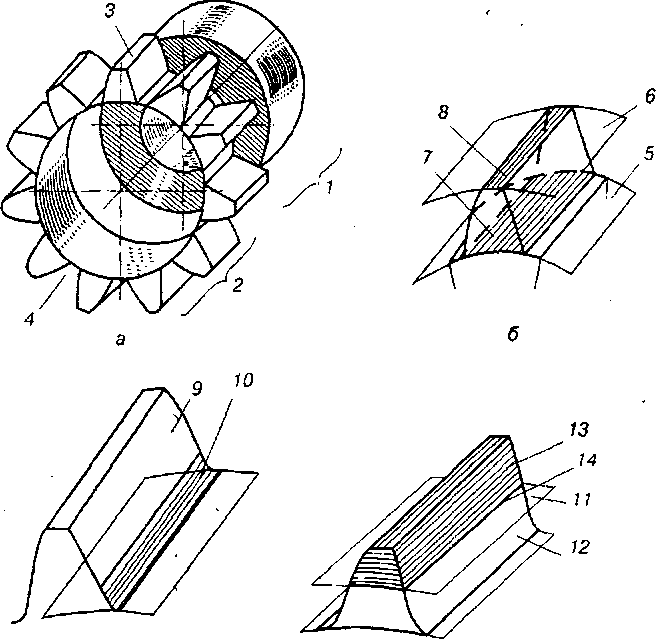
Рис. 9.7. Геометричні параметри циліндричного зубчастого колеса

Поверхня, яка обме­жує зуб з боку западин, називається бічною. Вона складається з головної 9 (рис. 9.7, в) і перехідної 10 поверхні. Головною будемо називати частину бічної поверхні, яка при взаємодії з такою самою поверхнею зуба іншого колеса може передавати рух із заданими швидко­стями. Поверхні елемен­тів вищої кінематичної пари, що забезпечують заданий рух, називаються спряженими поверхня­ми. Перехідна поверхня з'єднує головну поверх­ню з поверхнею западин. Частина головної поверх­ні, що взаємодіє з поверхнею зуба спряженого зубчастого колеса, нази­вається активною поверхнею зуба.

Враховуючи те, що зубчасті передачі циліндричними колесами – плоскі, всі її геометричні параметри можна розглядати в торцевому перетині (перпенди­кулярному до осі колеса). Тому розглядають замість поверхні западин коло запа­дин, поверхні вершин – коло вершин, головної та перехідної поверхонь зуба - го­ловний і перехідний профілі зуба, активної поверхні зуба - активний профіль зуба.

Розміри зубчастих коліс зручно задавати в частках певної ліній­ної величини, що пов'язана із зубом. Коловий крок для цієї функції не підходить, оскільки є ірраціональним числом. Такою величиною вибрано модуль т зубчастого колеса, який є відношенням колового кроку р до числа 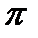. Отже:

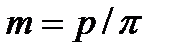. (9.5)

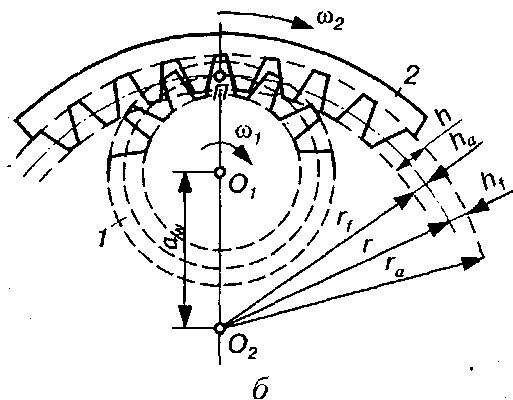
Модуль виміряється в міліметрах і є величиною стандартною. Щоб пояснити вибір цієї величини, виразимо довжину деякого кола діаметром d (рис. 9.8, а) через число зубів колеса z:

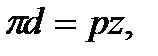
звідки

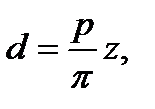
або з урахуванням (9.5), маємо

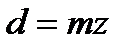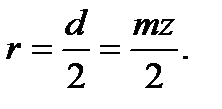або (9.6)

Модуль т для одного й того самого колеса, так само як і крок р, залежить від діаметра кола, до якого він відноситься. Прийнято коло, для якого знаходять стандартне значення модуля, називають ділильним [1]. З урахуванням (9.6) можна сказати, що ділильним називається коло, діаметр якого визначають добутком модуля на число його зубів.

Ділильна поверхня 11 ділить зуб на дві частини (рис. 9.7, г, 9.8, а): ділильну ніжку 12 і ділильну головку 13.

Висота ділильної ніжки

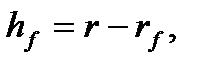(9.7)

ділильної головки

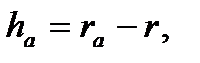(9.8)

повна висота зуба

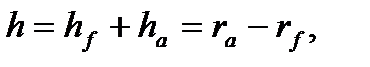(9.9)

де 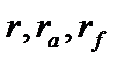– відповідно радіуси ділильного кола, кола вершин і западин.

Лінія 14 перетину бічної поверхні зуба з ділильною поверхнею (рис. 9.7, г) називається лінією зуба. Залежно від розташування лінії зуба від­носно осі колеса, як уже зазначалось, відрізняють прямий зуб (прямозубі ко­леса), лінія якого лежить в осьовій площині зубчастого колеса, і косий зуб (косозубі або шевронні колеса), лінія якого є гвинтовою лінією сталого кроку. За­лежно від напрямку гвинтової лінії косозубі колеса можуть бути праві або ліві.

Зубчаста рейка 2 (див. рис. 9.4, б) – це сектор циліндричного зуб­частого колеса, ділильний радіус якого нескінченно великий, у результаті цього ділильна поверхня (коло), поверхні вершин і западин, відповідні го­ловні бічні поверхні є паралельними площинами, тобто головний бічний профіль прямолінійний.

Для зубчастого колеса 2 із внутрішніми зубами (див. рис. 9.8, б) формули (9.7)-(9.9) набувають вигляду:

Для позначення геометричних і кінематичних параметрів зубчас­тих коліс і зубчастої передачі використовується система цифрових і літер­них індексів, які відносяться, зокрема, до:

0 - зуборізного інструменту та верстатного зачеплення;

1 - шестерні, черв'яка;

2 - колеса, черв'ячного колеса;

а - поверхні або кола вершин і головки зуба;

f - поверхні або кола западин і ніжки зуба;

b - основної поверхні (кола);

w - початкової поверхні, початкового кола або до загального ви­падку передачі;

е - зовнішнього торцевого перерізу конічного зубчастого колеса;

і- внутрішнього торцевого перерізу конічного зубчастого колеса;

т - середнього перерізу конічного зубчастого колеса;

х - основного перерізу або довільно назначеного перерізу;

у- довільно назначеного концентричного кола;

п - нормального перетину;

t - торцевого перетину;

l - граничної точки профілю зубів;

р - нижньої точки активного профілю.

Примітка: Якщо параметр відноситься до ділильної поверхні або ділильного кола, літерний індекс не ставиться. Встановлений такий поря­док проставлення складних індексів: на першому місці індекси п, t, х, на другому – у, w, а, f, на третьому - е, і, т для конічних передач, на четвер­тому–0, 1, 2.

У випадках, які виключають непорозуміння, допускається опуска­ти деякі індекси. Так, для прямозубих коліс виключають індекси tі п, для конічних – т. Якщо будь-які індекси пропускаються, то залишені перемі­щаються вперед. Якщо параметри відносяться взагалі до зубчастого коле­са, то індекси 1 або 2 опускають.

Верхній індекс * означає коефіцієнт, який характеризує відповід­ний параметр.

9.4. Основна теорема зубчастого зачеплення

Однією з найважливіших умов роботи зубчастого зачеплення є збереження за час контакту пари зубів заданого передаточного відношен­ня, тобто щоб початкові кола котились одне по одному без ковзання. Необхідно встановити, які вимоги повинні задовольняти спряжені профілі зубів, щоб забезпечити цю умову.

Розглянемо пару зубчастих коліс (рис. 9.9), що перебувають у за­чепленні. Нехай перше колесо є вхідним і обертається навколо нерухомої осі 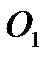із сталою швидкістю 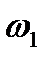, а друге – вихідне, його кутова швидкість 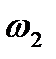, вісь обертання – 0₂. Точку контакту зубів позначимо через К, а її від­стані від осей обертання відповідно R₁ і R₂. При таких параметрах швид­кість точки К: першого колеса 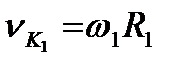, і спрямована перпендикулярно до радіуса другого колеса – 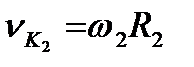і перпендикулярно до радіуса R₂.

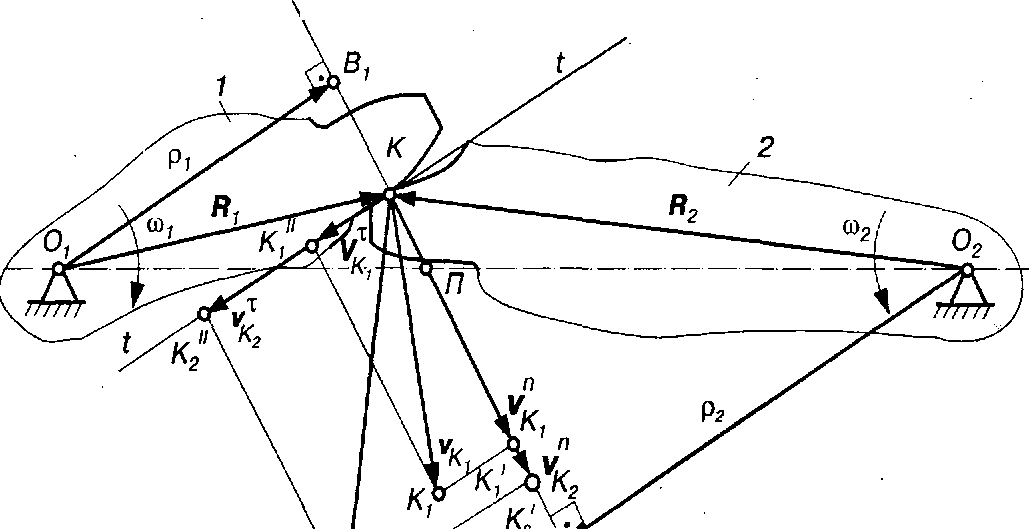
Рис. 9.9. До основної теореми зубчастого зачеплення

Розкладаємо вектори цих швидкостей на дві складові, які спряму­ємо вздовж спільної нормалі N – N, проведеної до профілів зубів через точку К, і вдовж спільної дотичної t – t, що також проходить через точку К.

Розглянемо складові швидкості точки К на спільну нормаль 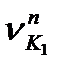і 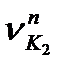та встановимо зв'язок між ними. Ці складові повинні бути рівними між собою( 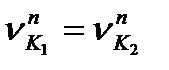); в інших випадках, якщо 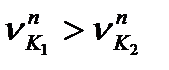, зуб першого колеса повинен проникнути в зуб іншого колеса, що неможливо; якщо 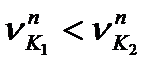, зуб першого колеса повинен відставати від зуба другого колеса і цим самим повинен порушуватися контакт, але цьому заважають зовнішні сили. Отже,для забезпечення безперервного контакту пари зубів необхідно, щоб проекції швидкостей точки контакту зубів на спільну нормаль були рівні між собою.

Із подібності трикутників 0₁В₁К і К 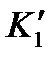К₁ та 0₂В₂К і КК'₂К₂ складемо пропорції:

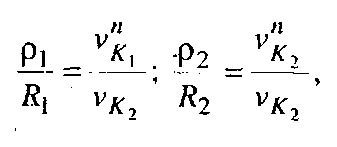
звідки маємо

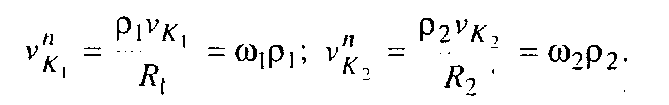
(9.10)

Враховуючи, що в цих рівностях ліві сторони тотожні, справед­лива й така рівність

,

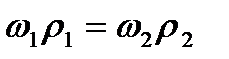звідки можна записати залежність для передаточного відношення

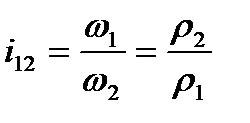. (9.11)

Нормаль NN перетинає лінію центрів 0₁0₂ у точці П, яка називається полюсом зубчастого зачеплення. Із подібності трикутників 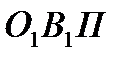і 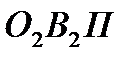маємо:

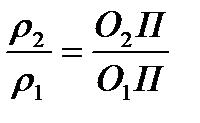. (9.12)

Тоді рівняння (9.11) можна записати в такому вигляді:

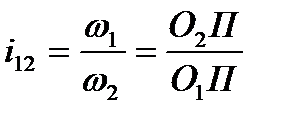. (9.13)

Рівність (9.13) виражає змістосновної теореми зачеплення(теореми Вілліса), яка формулюється так:активні профілі зубів двох коліс повинні бути побудовані так, щоб нормаль у точці їх дотику в будь- який момент зачеплення проходила через точку П (полюс зачеплення), що ділить лінію центрів у відношенні обернено пропорційному переда­точному відношенню.

Відстань між точками 0₁ і О₂ визначає міжосьову відстань

,

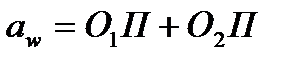а відрізки 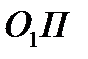і 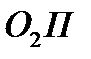є радіусами початкових кіл 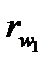і .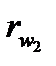

При змінному значенні передаточного відношення і₁₂ полюс зачеплення П займає на лінії центрів 0₁0₂ змінне положення, що спостерігається в зубчастих механізмах з некруглими колесами (рис. 9.10). При сталому значенні і₁₂ полюс за­чеплення завжди знаходиться в одній і тій самійточці П на лінії О₁О₂.

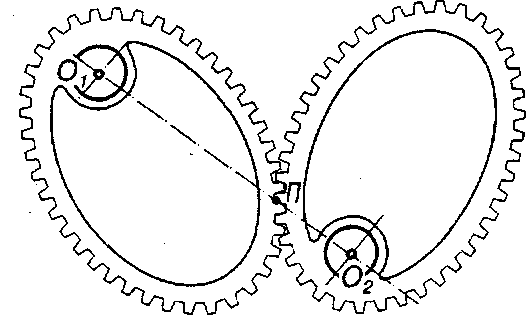
Рис. 9.10. Передача некруглими зубчастими колесами

Якщо кутові швидкост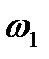і і 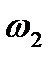мають різні знаки, то і₁₂<0 і полюс зачеплення П лежить між точками О₁ і О₂. Цей вид зачеплення називається зовнішнім. Якщо кутові швидкост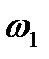і і 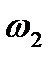мають один знак, то і₁₂<0 і полюс зачеплення П лежить за межами відрізка О₁О₂ (див. рис.9.8, б). Такий вид зачеплення називають внутрішнім.

Теоретично для того, щоб забезпечити основну теорему зачепленню профілі зубів можна побудувати різними кривими. У техніці (особливо в машинобудуванні) найбільше поширений евольвентний профіль зубів, рідше використовується цикло­їдне зачеплення (в основному у приладобудуванні та годинниковій промисловості).