ЗАКОНОМІРНОСТІ СТИСНЕНОГО РУХУ ТІЛ У СЕРЕДОВИЩІ

При масовому русі частинок під впливом тих же сил, що і при вільному падінні, виникають більш складні гідродинамічні явища, обумовлені перемішуванням частинок у подовжньому і поперечному напрямках, тертям частинок одна об одну і стінки апарата, виникненням висхідних потоків середовища в проміжках між частинками. У результаті цього виникають додаткові сили опору, що різко змінюють характер руху кожної окремої частинки, унаслідок чого швидкість руху частинки значно зменшується.

Вивчення закономірностей стисненого падіння частинок базується на двох концепціях:

- перша концепція розглядає стиснене падіння як груповий рух частинок, що являють собою фільтраційне середовище, крізь яке рідина протікає у вертикальному напрямку знизу вгору;

- друга концепція розглядає стиснене падіння як падіння окремої частинки, що знаходиться в масі інших, при цьому за основу приймається швидкість вільного падіння, а умови стиснення враховуються поправочними коефіцієнтами.

Відповідно до цих концепцій запропоновано багато формул для визначення швидкості стисненого руху зерен у середовищах.

Формули, що базуються на першій концепції, громіздкі, незручні для інженерного розрахунку, тому вони застосовуються значно рідше формул, що базуються на другій концепції.

Найбільш розповсюдженою формулою, що базується на другій концепції, є формула:

V_cm = V₀ Θ ^m, (2.30)

де V_cm і V₀ – швидкості стисненого і вільного падіння, м/с; Θ –коефіцієнт розпушення, частки од.; m – показник степеня, що залежить від розміру, густини і форми частинок, а також від співвідношення розмірів частинок і апарата, у якому відбувається розділення, вінприймає значення: m = 1 – у формулі Фінкея, m = 2 у формулі Ханкока, m = 3 – у формулі Лященка.

Величина показника степеня m змінюється від 4,65 до 2,39 у діапазоні чисел Рейнольдса 0,3 – 500, поза цим діапазоном величина показника степеня має постійне значення: при Re < 0,3 m = 4,65;при Re > 500 m = 2,39.

Швидкості, розраховані за формулою Фінкея, завищені, за формулою Лященка – занижені. Формула Ханкока для частинок крупністю 0,1 – 12,5 мм дозволяє одержати результати близькі до фактичних.

Запропоновано ряд інших формул ряд формул для визначення швидкості стисненого падіння залежно від густини середовища, об'ємного вмісту твердої фази в пульпі:

– формула Річардса: V_cm= 0,174 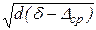, м/с; (2.31)

– формула Стокса-Ейнштейна: V_cm= V₀ / (1 – 2,5 С), м/с; (2.32)

– формула Загустіна: V_cm= V₀ (1 – 2,5 С) , м/с (2.33)

– формула Годена: V_cm= V₀ (1 – С^0,67)(1 – С)(1 – 2,5 С) , м/с, (2.34)

де С– об'ємна концентрація твердої фази, частки од.

Формули (2.32) – (2.33) можуть бути використані при розрахунку швидкостей частинок крупністю d > 1 мм, формула (2.34) – частинок крупністю d < 0,1 мм і об'ємної концентрації твердої фази С ≤ 0,3.

За методом Т.Г.Фоменка для обчислення швидкості стисненого падіння спочатку визначають параметр Архімеда (2.20), а потім по кривій ψ_ст = f (Ar) (рис. 2.5) або за формулою (2.35) знаходять коефіцієнт ψ_ст:

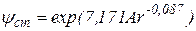; (2.35)

Після визначення ψ_ст розраховують швидкість стисненого падіння за формулою (2.22), замінивши в ній V₀ на V_cm і ψ на ψ_ст. Результати розрахунку близькі до фактичного в діапазоні крупності частинок від 0,05 до 12,5 мм.

Коефіцієнт рівнопадання в умовах стисненого падіння визначається з урахуванням додаткових сил опору, що враховується заміною у формулі (2.24) густини рідини Δ на густину середовища Δ_СР:

e = [(δ₂ – Δ_СР) / (δ₁ – Δ_СР)] ⁿ . (2.36)

За методами П.В.Лященка та Т.Г.Фоменка визначення коефіцієнта рівнопадання при стисненому падінні виконується за тією ж методикою, що й при вільному, але з поправкою на густину середовища, що змінилася.

Коефіцієнт рівнопадання частинок у стиснених умовах значно більший, ніж у вільних, що дозволяє розширити шкалу класифікації. Наприклад, для вугілля і породи у вільних умовах він дорівнює 3, а в стиснених умовах – 12.