Ковзання профілів зубів

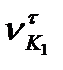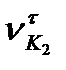Розглянемо тепер інші складові швидкості точки контакту – і . Ці складові не рівні між собою, інакше повинні бути рівні між со­бою швидкост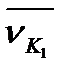і і 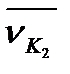як за величиною, так і за напрямком. Як видно з рис. 9.9, така рівність можлива лише в одному положенні механізму, коли точка К контакту зубів буде збігатися з полюсом П. Для всіх інших положень ланок передачі 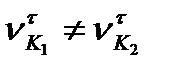. У результаті цього має місце відносне ковзання профілів зубів у напрямку їх спільної дотичної t-t. Ковзання зубів є основною причиною втрат енергії на тертя і спрацювання зубів.

Як видно з рис. 9.9, швидкість ковзання профілів зубів

. (9.14)

Можна показати, що для зовнішнього зачеплення

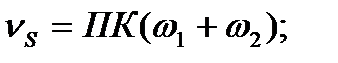(9.15)

для внутрішнього зачеплення

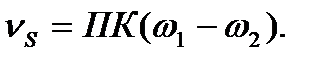(9.16)

Отже, чим далі розташована точка контакту к~ відносно полюса за­чеплення П, тим більша швидкість ковзання.

При одній і тій самій швидкості ковзання спрацювання в спряже­них профілях може бути різним. Для кількісної оцінки спрацювання вво­диться поняття питомого ковзання зубів, під яким розуміють відношен­ня швидкості ковзання 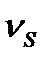точки контакту зубів до дотичної складової 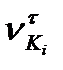швидкості точки контакту відповідного колеса (і = 1; 2), тобто

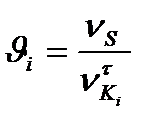. (9.17)

На рис. 9.11 показано при­клади діаграм питомого ковзання 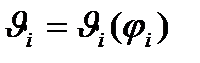. При цьому треба врахо­вувати, що кут повороту зубчастого колеса пропорційний відрізкам лінії В₁В₂ (див. рис. 9.9), яка називається теоретичною лінією зачеплення.

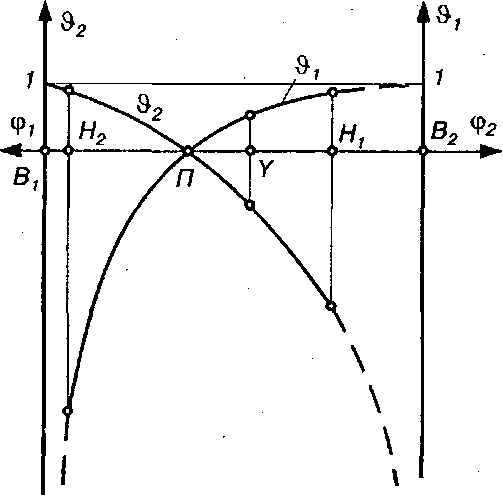
Рис.9.11. Діаграми питомого ковзання профілів зубів

У полюсі зачеплення пито­ме ковзання дорівнює нулю, отже профілі перекочуються один по од­ному без ковзання.

На початкових головках зу­бів, що розташовані між колом вершин і початковим колом, питоме ковзання невелике; на початкових ніж­ках (між початковим колом і колом западин) питоме ковзання значно більше, ніж на початкових головках. На початковій ніжці першого колеса (шестірні) питоме ковзання 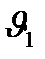значно більше, ніж на початковій ніжці іншого колеса. Це означає, що спрацювання ніжки зуба шестірні буде при роботі передачі значно більшим, ніж спрацювання початкової ніжки зуба колеса.

9.6. Властивості й рівняння евольвенти кола

Для побудови головного профілю зубів циліндричних зубчастих коліс, що використовуються в машинобудуванні, найперше застосовується евольвентний профіль. Плоскою евольвентою кола називають траєкторію будь-якої точки, наприклад А (рис. 9.12), прямої лінії, яка перекочується без ковзання по колу радіуса 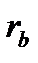; таке коло називають еволютою або ос­новним, а пряму – твірною прямою.

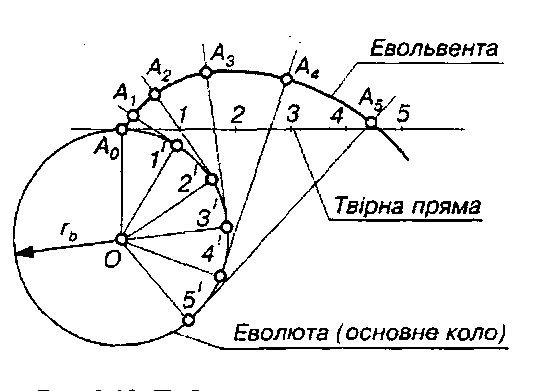
Рис. 9.12. Побудова евольвенти кола

Побудова евольвенти кола на­ступна. Спочатку проводимо до основ­ного кола твірну пряму, яка дотикається до нього в точці А₀. Потім перекочуємо твірну пряму по основному колу без ковзання. Для цього від точки А₀ відкла­даємо на твірній прямій ряд однакових відрізків А₀1, 12, 23 і т.д. На основному колі від цієї ж точки відкладаємо дуги 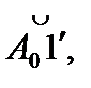і т. д., що дорівнюють цим відрізкам.

При перекочуванні прямої по колу без ковзання точка 1 збігається з точкою 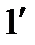, точка 2 – з точкою 2' і т.д. Проведемо через точки 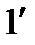, 2', 3' і т.д. до­тичні до кола (для точної побудови дотичної слід спочатку провести радіус у відповідну точку, а потім провести до нього перпендикуляр) і відкладаємо на них з точок дотику відрізки 1'А₁, 2'А₂, 3'А₃ і т.д., що дорівнюють відповідно відрізкам прямої А₀1, А₀2, А₀З і т.д. 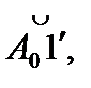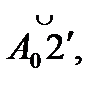(або дугам 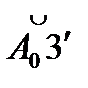і т.д.). З'єднуючи точки А₀, А₁, А₂ і т.д. плавною кривою, одержимо евольвенту.

Широке використання евольвенти при проектуванні профілів зубів пояснюється низкою важливих властивостей. Відмітимо основні власти­вості евольвенти.

1. Твірна пряма завжди нормальна до евольвенти. Дійсно, точка дотику твірної прямої з основним колом є при утворенні евольвенти мит­тєвим центром обертання твірної прямої, а тому відповідні відрізки (1'А₁, 2'А₂, 3'А₃ і т.д.) є миттєвими радіусами кривизни евольвенти. Оскільки ра­діус кривизни завжди розміщений нормально до кривої то твірна пряма завжди нормальна до евольвенти.

2. Форма евольвенти залежить тільки від радіуса основного кола, тобто не залежить від параметрів спряженого колеса – це дає змогу використовувати евольвентні зубчасті колеса в коробках передач, тобто у ме­ханізмах із змінними зубчастими колесами, в яких з одним колесом мо­жуть входити у зачеплення колеса з різним числом зубів.

3. Евольвента починається на основному колі і завжди розташо­вана за його межами.

4. Радіус кривизни на початку евольвенти (на основному колі) до­рівнює нулю, а радіус основного кола, проведений через початок евольвен­ти, є плавним продовженням евольвенти всередині основного кола.

5. Дві евольвенти одного основного кола є еквідистантнгіми (рівновіддаленими) кривими, а відстань між ними по спільній нормалі для відповід­них профілів двох сусідніх зубів є евольвентним кроком 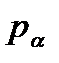і дорівнює дов­жині дуги кола між початками кривих, тобто дорівнює основному кроку .

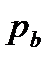Евольвента має дві вітки. Додатну вітку одержуємо при переко­чуванні твірної прямої проти руху годинникової стрілки, від'ємну – при перекочуванні за рухом годинникової стрілки.

Рівняння евольвенти одержуємо з умови перекочування твірної прямої по основному колу без ковзання. Для цього розглянемо деяке до­вільне положення твірної прямої (рис. 9.13), яке відповідає точці Y еволь­венти. Нехай координатами точки Y будуть: 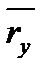– радіус-вектор і 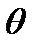– кут відхилення радіуса-вектора 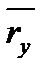від радіуса 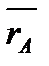, що проведений через поча­ток евольвенти А. Проводимо через точку Y дотичну до основного кола радіуса 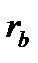. Точка дотику М є для евольвенти у точці Y центром кривизни, а відрізок МY – її миттєвим радіусом кривизни. Точку М з'єднаємо з центром основного кола О і позначимо кут між променями ОМ і ОY через 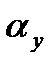. Цей кут дорівнює куту профілю, під яким розуміють гострий кут між дотичною до профілю у відповідній точці Y і радіусом-вектором цієї точки . Очевидно, що кут профілю 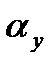дорівнює куту МОY, оскільки лінія ОМ і дотична у точці Y паралельні одна одній.

Із трикутника ОМY маємо

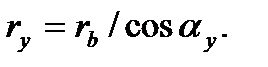(9.18)

Оскільки евольвента одержана перекочуванням твірної прямої відносно основного кола без ковзання, то МY = 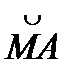. Враховуючи, що 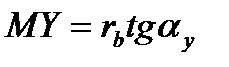і 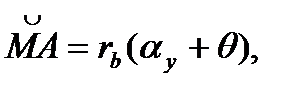одержимо

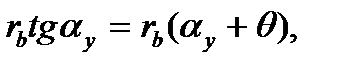
або

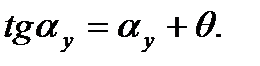
Розв'язуючи це рівняння від­носно 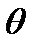, одержимо

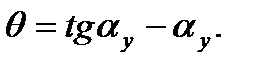
Вираз 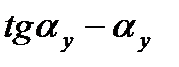скорочено позначають inv 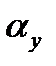і читають «інволюта альфа-ігрек»:

inv 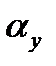= 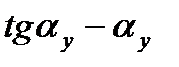(9.19)

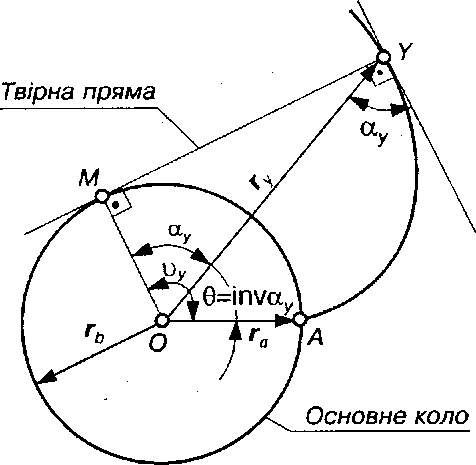
Рис. 9.13. До виводу рівняння евольвенти

Кут inv 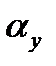= 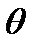називається евольвентним кутом, він позначає кут між радіусами, що проведені через початок евольвенти А і точку Y. Для інволютної функції складені таблиці, з яких за значеннями кута 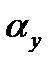можна визначити функцію inv 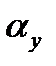, або навпаки.

Рівняння (9.18) і (9.19) є рівняннями евольвенти кола в параме­тричному вигляді.

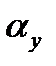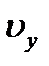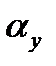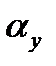Зазначимо, що положення точки Y на евольвенті можна задати будь-яким кутом із кутів , = +inv , inv 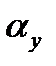або радіусом-вектором , що проходить через початок евольвенти А і радіусом 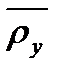= МY, проведеним через центр кривизни М евольвенти у точці Y.

Радіус кривизни евольвенти у точці Y

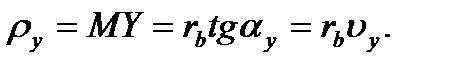(9.20)

9.7. Теоретичний вихідний і твірний контури

Одним із багатьох важливих факторів, які лежать в основі досягнень сучасної техніки, є взаємозамінність, тобто здатність спряжених деталей з'єднуватись одна з одною без спеціальної пригонки або підбору. Взаємо­замінність можлива лише на базі стандартизацій тобто при суворій регла­ментації форми, розмірів, якості й точності різних деталей та виробів.

Зубчасте колесо – одна із найскладніших і точних деталей машин; для його виготовлення вимагається спеціальне дороге обладнання, різаль­ний та вимірювальний інструмент. Тому стандартизація параметрів зуб­частого зачеплення важлива як з технічної, так і економічної точки зору.

За базу при стандартизації зубчастих коліс можна прийняти різні параметри. На основі багатолітньої практики при стандартизації коліс і зуборізального інструменту в усіх країнах світу приймають параметри зубчастої рейки з прямолінійним профілем (рис. 9.14). Рейковий профіль, який покладено в основу стандарту, називається теоретичним вихідним контуром (ТВК) або коротко – вихідним контуром. Параметри вихідного контуру стандартизовані (ГОСТ 13755-68). Це прямобічний рейковий кон­тур із рівномірно розташованими симетричними зубами трапецієподібної форми; перехід від профілю зуба до лінії западин викреслений дугою кола. За базу для визначення елементів зубів та їх розмірів вибирають ділильну пряму (площину), яка перпендикулярна до осей симетрії зубів рейки і товщина зуба на ній дорівнює ширині западини {а=е=р/2). Частина зуба, що знаходиться між ділильною поверхнею і поверхнею вершин, назива­ється ділильною головкою зуба; а частина зуба між ділильною поверхнею і поверхнею западин – ділильною ніжкою зуба.

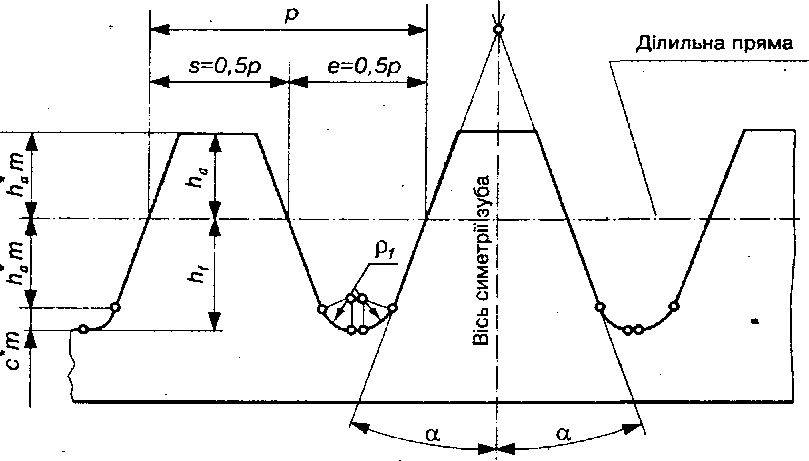
Рис.9.14. Теоретичний вихідний контур

Відстань між однойменними профілями сусідніх зубів по ділиль­ній або будь-якій іншій паралельній прямій називають кроком р вихідного контуру (9.5):

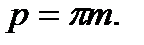(9.21)

Висота ділильної головки зуба вихідного контуру

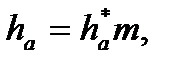(9.22)

де 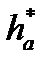– коефіцієнт висоти головки зуба (відношення висоти головки зуба до модуля: ).

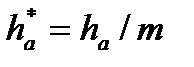Ділильна ніжка зуба 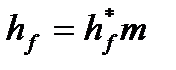вища від головки на величину 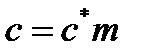– радіальний зазор, де с* – коефіцієнт радіального зазору (с* =с/m). Отже, коефіцієнт висоти ніжки зуба 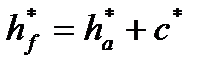, а висота ділильної ніжки зуба

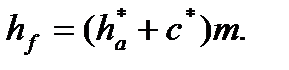(9.23)

Кут 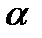між бічною стороною та віссю зуба називається кутом профілю вихідного контуру.

ГОСТ 13755-68 регламентує параметри вихідного контуру:

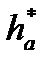= 1,0; с* = 0,25; 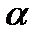= 20°.

При цьому висота зуба

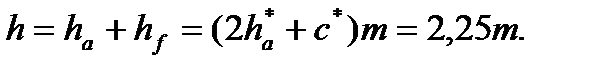(2.24)

Прямолінійний профіль вихідного контуру плавно спряжений з лінією його западин дугою радіуса

(9.25)

де 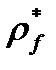– коефіцієнт радіуса перехідної кривої( 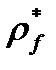= 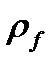/т).

Геометричні параметри різального інструменту визначаються вихідним твірним (виробничим) контуром (ВТК), або коротко – твірним контуром (рис. 9.15). Вихідним твірним рейковим контуром на­зивають контур зубів рейки, який ніби заповнює западини теоретичного вихідного профілю, як відливка заповнює форму. При цьому між лінією западин твірного контуру й лінією вершин вихідного зберігається радіальний зазор с=с*т для того, щоб поверхня западин різального інструмента не брала участі в процесі різання. У межах цього зазору збері­гається також перехід по дузі кола від профілю зуба до лінії западин ВТК.

Таким чином, вихідний твірний контур має ділильну ніжку такої самої форми та розмірів, як і вихідний контур. Для одержання радіального зазору в зубчастому зачепленні ділильна головка твірного контуру виго­товляється вищою за головку вихідного контуру на величину с. Отже, ділильна пряма твірного контуру ділить зуб по висоті на дві рівні частини а повна висота зуба

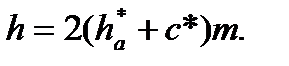(9.26)

Колесо із зовнішніми зубами, нарізане твірним рейковим конту­ром при збереженні на ділильному колі теоретичної товщини зуба 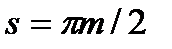і теоретичного радіального зазору ст у западині рейки, нази­вають твірним зубчастим колесом. Таке колесо служить різальним ін­струментом при зубодовбанні.

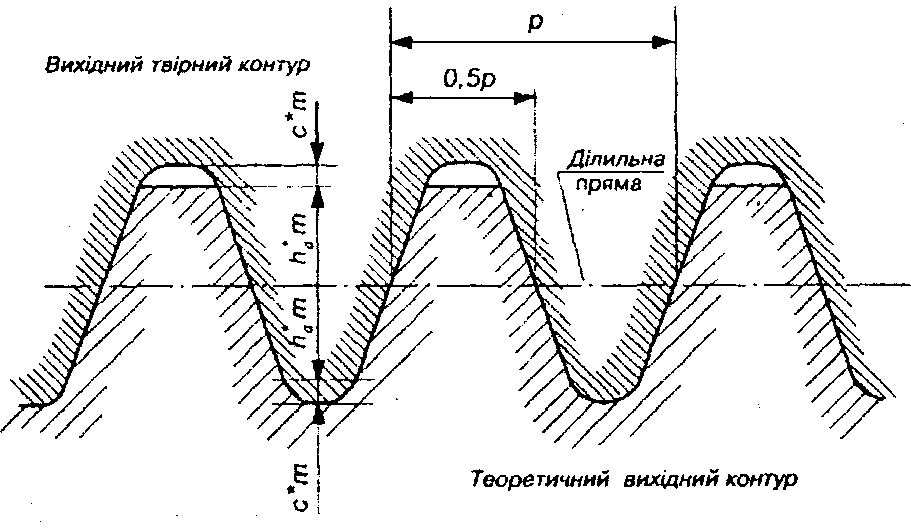
Рис. 9.15. Вихідний твірний (виробничий) контур

9.8. Деякі відомості про способи нарізання зубчастих коліс

Зубчасті колеса можна виготовляти різними способами: різан­ням, литвом, пластичною деформацією (штамповка або накатка). Найбільш точні зубчасті колеса одержують різанням з використанням доводочних операцій.

Існує два принципово різні способи нарізання зубів: копіювання та обкатки.

Спосіб копіювання. При цьому способі зубчасті колеса нарі­зають інструментом, профіль якого точно збігається з профілем запа­дин колеса, що нарізається, тобто профіль інструмента копіюється на колесі (рис. 9.16, а, б, в). Інструментом може бути модульна (дискова або пальцьова) фреза. Обертаючись, фреза пересувається вздовж зуба. За кожний хід фрези нарізається одна западина. Після цього заготовка повертається на кутовий крок 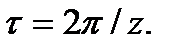Цим методом можна нарізати прямозубі, косозубі та шевронні зубчасті колеса, для останніх заготовка в процесі нарізання повертається на відповідний кут.

Рис. 9.16. Нарізання зубчастих коліс

Використовують також інструмент, що обробляє всі западини одночасно – протяжки, зубодовбальні головки тощо.

Основний недолік способу копіювання полягає в тому, що різаль­ний інструмент є фасонним, тобто має криволінійні різальні кромки і при його виготовленні неминучі похибки, які передаються колесу, що нарізаєть­ся. Крім цього, при використанні набору модульних фрез доводиться навми­сно вносити ще й додаткові похибки за таких причин: діаметр основного кола, за евольвентою якого обкреслений профіль зубів, визначається моду­лем т і числом зубів z колеса, що нарізується. Очевидно, що для кожного сполучення т і z треба мати окрему фрезу; оскільки в стандарті більше 50 модулів, а число зубів, які використовуються, перевищує 100, то в універ­сальному комплекті повинно бути поцад 5000 фрез. Для скорочення номен­клатури інструменту діапазон чисел z розбивають на інтервали і в межах кожного інтервалу використовують одну і ту саму фрезу для нарізання коліс з різними числами зубів. Для кожного модуля комплект складає 8-15 фрез.

Через низьку точність коліс і малу продуктивність процесу нарі­зання методом копіювання доцільно цей метод використовувати лише в індивідуальному або дрібносерійному виробництвах для виготовлення малонавантажених і тихохідних передач.

Шліфувальні круги, різці й протяжки профілюють для кожного конкретного колеса, і похибки, викликані невідповідністю інструмента числу зубів колеса, що нарізаються, у цьому випадку відсутні.

Недоліком методу копіювання є також те, що для реалізації будь-якої зміни в геометрії зубів необхідно виготовляти спеціальний інстру­мент, що пов'язано із значними трудовими і матеріальними затратами.

Процес нарізання зубів протяжками та зубодовбальними головка­ми продуктивний, але через складність і високу вартість інструменту доцільно такий процес використовувати лише в масовому виробництві.

Спосіб обкатки (огинання). При цьому способі в основу геометрії інструмента покладено так зване твірне колесо або рейку, бічні поверхні зубів яких мають різальні кромки.

При нарізанні зубів твірному колесу (інструменту) і колесу (заго­товці), що нарізається, надають такого відносного руху, який би мали ці коле­са, перебуваючи в зачепленні один з одним. Зачеплення твірного колеса з оброблюваним колесом називають верстатним зачепленням. Отже, у верстатному зачепленні відтворюється перекочування без ковзання почат­кових поверхонь інструмента й колеса, що нарізається, – чим і пояснюєть­ся назва способу обкатки.

На рис. 9.16, г зображено нарізання зубів евольвентним твірним колесом (зуборізним довбачем). Довбач 1 здійснює поступальний рух паралельно осі колеса (заготовки) 2, що нарізається. Одночасно довбачу та заготовці надають обертового руху з тим самим відношенням швидкостей які б мали довбач і колесо, знаходячись у зачепленні. Тоді профіль зуба виходить як огинаюча всіх положень ріжучої кромки довбача(рис. 9.16, є). Особливість цього методу полягає в тому, що він дає можливість нарізати колеса з внутрішніми зубами (рис. 9.16, д).

Оскільки для будь-якого зубчастого колеса може бути спроекто­вана спряжена з колесом зубчаста рейка, то замість колеса-інструмента може бути інструментом також і рейка, яка називається інструменталь­ною рейкою або гребінкою. У процесі нарізання рейка здійснює вздовж осі заготовки зворотно-поступальний рух (рис. 9.16, е). Заготовка має подвій­ний рух у горизонтальній площині: обертовий навколо своєї осі і посту­пальний вздовж рейки. Отже, заготовка здійснює рух колеса відносно рей­ки, і профілі зубів колеса одержують як обкатку цих ланок. Весь цей про­цес здійснюється на спеціальних зубодовбальних верстатах.

Гребінка – найпростіший, а тому найточніший інструмент рейко­вого типу. Проте число зубів гребінки обмежене, оскільки довгі гребінки важко виготовляти, а число зубів коліс, що нарізаються, частіше всього більше від числа зубів гребінки, то процес обкатки не може бути безпе­рервним. Після того, як заготовка перекотилась по всій довжині гребінки, процес обкатки припиняється, заготовку повертають у вихідне положення і продовжують обкатку. Таке періодичне переривання зменшує точність і продуктивність зубонарізання, ускладнює верстат.

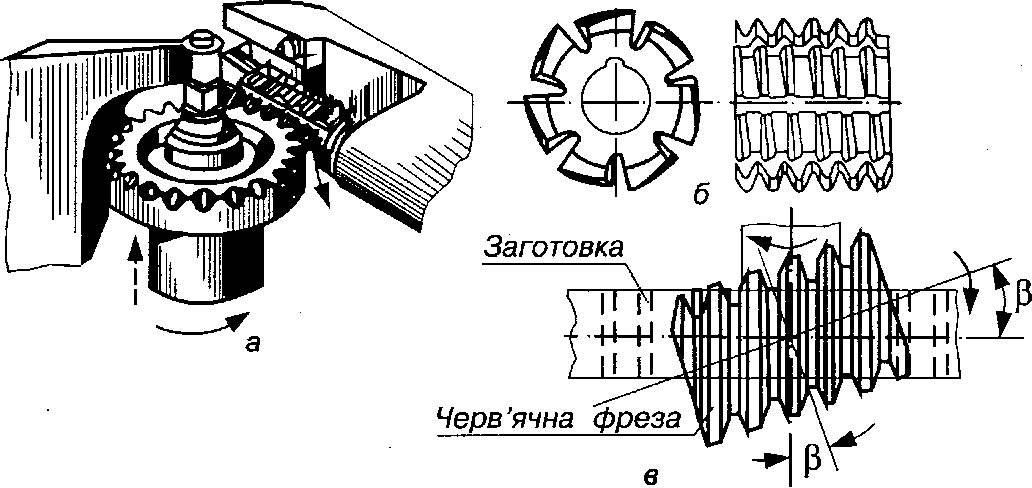
Рис. 9.17. Нарізання зубчастих коліс за допомогою черв'ячної фрези

Для того, щоб зробити процес обкатки безперервним, використо­вують черв'ячні фрези. Черв'ячна фреза (рис. 9.17, б) – це гвинт із трапецеподібною різьбою (рис. 9.17, в), профіль якої в нормальному перетині такий самий, як і профіль твірної рейки. Для утворення різальних кромок уздовж осі прорізані канавки (рис. 9.17, б). Зачеплення фрези з колесом, що нарізається, аналогічне зачепленню черв'яка з черв'ячним колесом (рис. 9.17, а). При цьому фреза та заготовка одержують обертовий рух, який би вони мали, перебуваючи в зачепленні. Щоб нарізати зуб по всій ширині зубчастого вінця, фреза (або заготовка), крім обертання, одержує гїодачу вздовж осі колеса. Фреза встановлюється відносно заготовки так, щоб її витки в місці знімання стружки були паралельні твірній циліндра- заготовки (рис. 9.17, в), тобто вісь фрези повинна утворювати з торцевою поверхнею заготовки кут 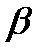, який дорівнює куту підйому середньої лінії гвинтової поверхні витків фрези.

Останніми роками поширився новий метод обкатки – накатка зубчастих коліс у холодному (для дрібномодульних коліс, т 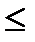2 мм) або в гарячому стані, який полягає в наступному. Інструмент у вигляді зуб­частого колеса і заготовка одержують на верстаті такі відносні рухи, ніби вони перебувають у дійсному зачепленні. При цьому завдяки пластичній деформації інструмент формує на заготовці зуби евольвентного профілю.

Значною перевагою всіх методів обкатки є висока продуктивність, велика точність і мала кількість інструменту. Одним інструментом (даного модуля) можна нарізати зубчасті колеса з будь-яким число зубів та зміню­вати геометрію зубчастих коліс.

9.9. Розрахунок геометричних параметрів циліндричних прямозубих зубчастих коліс

Геометричні параметри циліндричних прямозубих зубчастих коліс залежать не тільки від їх модуля і чисел зубців, а й від положення металорізального інструменту відносно заготовки. Для цього розгляне­мо зачеплення зубчастого колеса, що нарізається, з прямозубою твір­ною рейкою, у процесі якого на заготовці формуються зуби відпові­дної геометрії та розмірів. Таке зачеплення називається верстатним зачепленням (див. п. 9.8). Картину зачеплення будемо розглядати в торцевому перетині (рис. 9.18, а).

У рейковому зачепленні рейка здійснює поступальний рух, а коле­со – обертовий. Такі ж рухи повинні виконувати ланки верстатного зачеп­лення. Необхідну швидкість 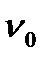руху твірної рейки, яка спрямована пара­лельно ділильній прямій, визначають із співвідношення

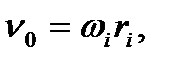(9.27)

де 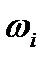– кутова швидкість заготовки; 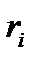– радіус ділильного кола зубчастого колеса, що нарізається. У цій формулі й далі індекс 0 позначає параметри різального інструменту, а індекс i = 1 або i = 2 відповідно шестірні або колеса. Індекс i може бути опущений, коли його значення неістотне.

Із формули (9.27) випливає, що при нарізанні зубчастого колеса рейковим інструментом ділильне коло є центроїдою у відносному русі твірного контуру і торцевого перетину заготовки. Інакше кажучи, у проце­сі нарізання деяка лінія твірного контуру, що дотикається ділильного кола, перекочується по ньому без ковзання. Така пряма твірного контуру нази­вається початковою. На рис. 9.18, а ділильна пряма 1 знаходиться на відстані х_іт від ділильного кола, а значить, від початкової прямої 2. Ця відстань називається зміщенням вихідного твірного контуру, де х_i=х_іт/m називається коефіцієнтом зміщення. Зміщення вважається додатним, якщо ділильна пряма і ділильне коло не перетинаються.

Зубчасті колеса, зуби яких утворені при х=0, тобто коли початкова пряма твірного контуру є його ділильною прямою, називаються зубчас­тими колесами без зміщення (інколи - нульовими). При х 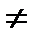0 одержуємо зубчасті колеса із зміщенням.

Практично нарізання коліс із зміщенням ніяких ускладнень не ви­кликає і досягається встановленням інструмента на відповідній відстані від осі заготовки. Можливість вибору зміщення при нарізанні зубчастих коліс дозволяє керувати у широких межах геометричні та якісні характеристики передач. Для вибору коефіцієнтів зміщення можна використовувати табличні методи і метод «блокувальних контурів» [5, 7, 10].

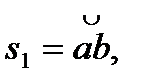
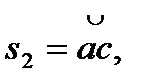
На рис. 9.18,6 зображені профілі зубів трьох коліс, що мають однакову кількість зубів, нарізані одним і тим самим інструментом, але з різним зміщенням: х₁<х₂<х_з. Колеса мають однакові радіуси ділильного й основного кіл, а значить, профілі зубів усіх трьох коліс окреслені однією й тою самою евольвентою, але товщини зубів 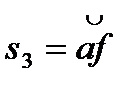і радіуси кіл вершин 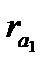, , 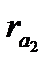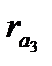у ко­ліс будуть різні. Із збільшенням коефіцієнта зміщеннях товщина зуба біля основи збільшується, а біля вершини зменшується, тобто коефіцієнт зміщення суттєво впливає на форму зуба. Отже, з трьох зубів, що розглядаються, зуб третього колеса буде найміцнішим. Крім цього, для евольвентної частини профілю зуба третього колеса використовується ділянка евольвенти, яка найбільш віддалена від її основи і має більший радіус кривизни, що сприяє зменшенню спрацювання і контактних напружень бічної поверхні зуба. Таким чином, вибираючи при проектуванні той чи інший коефіцієнт зміщення, можна впливати на форму зубів і на якість зубчастої передачі наділяючи її необхідними властивостями. Проте слід зауважити, що така залежність форми зубів і властивостей передачі від коефіцієнта зміщення х суттєво відчутна при малих числах зубів і послаблюється в міру збільшення z.

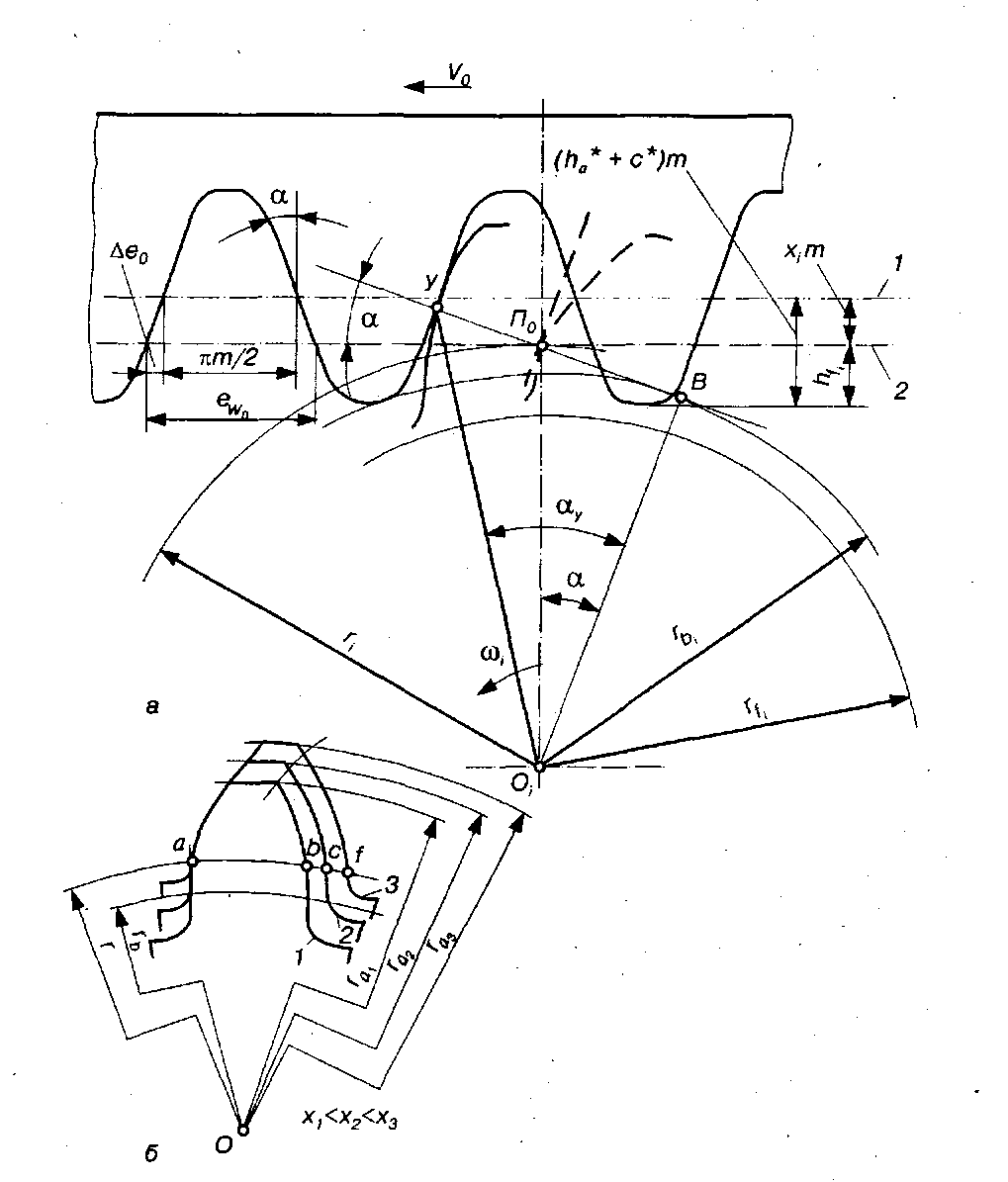
Рис. 9.18. Картина верстатного зачеплення (а) і вплив коефіцієнта зміщення на профіль зубів (б)

Враховуючи, що початкова пряма інструмента обкочується без ковзання по ділильному колу заготовки, крок зубів твірного контуру слід відкласти 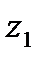разів на ділильному колі зубчастого колеса, яке нарізається. Причому зміщення інстру­мента відносно заготовки не змінює кроку по дузі ділильного кола (ділильного колового кроку), оскільки крок рейки по будь-якій прямій, паралельній ділильній, залишається сталим (див. рис. 9.14) – 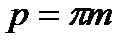, змінюється лише співвідношення між товщиною зуба 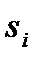і шириною западини 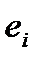зубчастого колеса ( ).

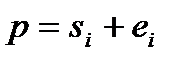При обкатці зубчастого колеса рейковим інструментом зуб рейки профілює западину, а западина – зуб колеса, що нарізається. Оскільки всі розміри початкової прямої твірної рейки переносяться без зміни на дугу ділильного кола, товщина зуба колеса по цій дузі 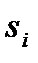(ділильна колова тов­щина зуба) дорівнює ширині западини 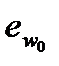рейки на початковій прямій. При зміщенні x_im (рис. 9.18, а) ширина западини рейки на початковій прямій

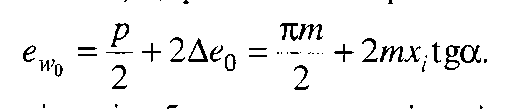
Тому при нарізанні зубчастого колеса із зміщенням x_im ділильна колова товщина його зуба

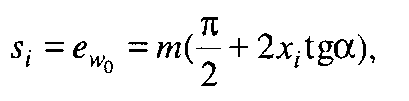
(9.28)

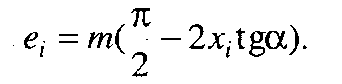а ширина його западини (ділильна колова ширина западини)

(9.29)

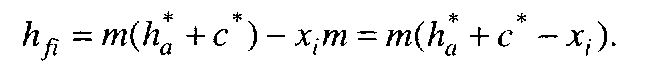Дно западини зубчастого колеса профілюється вершиною зуба твірної рейки. Тому розмір ділильної ніжки зубчастого колеса визначаєть­ся глибиною проникнення зуба рейки в заготовку. Згідно з рис. 9.18, а

(9.30)

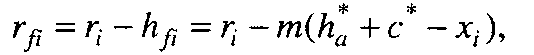Тоді радіус кола западин

(9.31)

де – радіус ділильного кола зубчастого колеса ( ).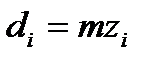

Для знаходження радіуса основного кола 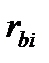використаємо основ­ну теорему зачеплення, згідно з якою спільна нормаль у точці дотику Y спряжених профілів (рейки і колеса) повинна проходити через полюс верстатного зачеплення і бути дотичною до основного кола (див. п. 9.4). Тому перпендикуляр О_іВ до нормалі YП₀ буде радіусом 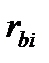основного кола зубчастого колеса, яке нарізається. Враховуючи, що перпендикуляр 0_iВ і профіль рейки паралельні, то кут П₀ОiВ дорівнює куту профілю 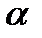вихід­ного твірного контуру.

Тоді з трикутника ОіП₀В знаходимо

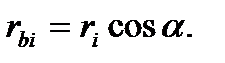(9.32)

Необхідно зазначити, що в момент збігання профілю рейки з полюсом П₀ (штрихова лінія) буде профілюватися точка евольвенти, що лежить на ділильному колі. Як видно з рисунка, кут профілю зуба колеса у точці, що лежить на ділильному колі, дорівнює куту 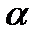твірного контуру. Кут профілю у точці Y позначимо .

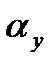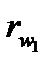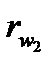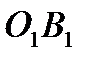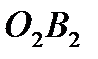При щільному зачепленні зубчастих коліс (без бічного зазору між зубами), що нарізані зі зміщенням твірного контуру тх_i , центроїдами у відносному русі будуть початкові кола радіусів і (рис. 9.19). Радіуси цих кіл можна визначити з трикутників П і П:

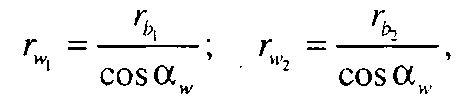
(9.33)

де 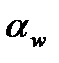– кут зачеплення.

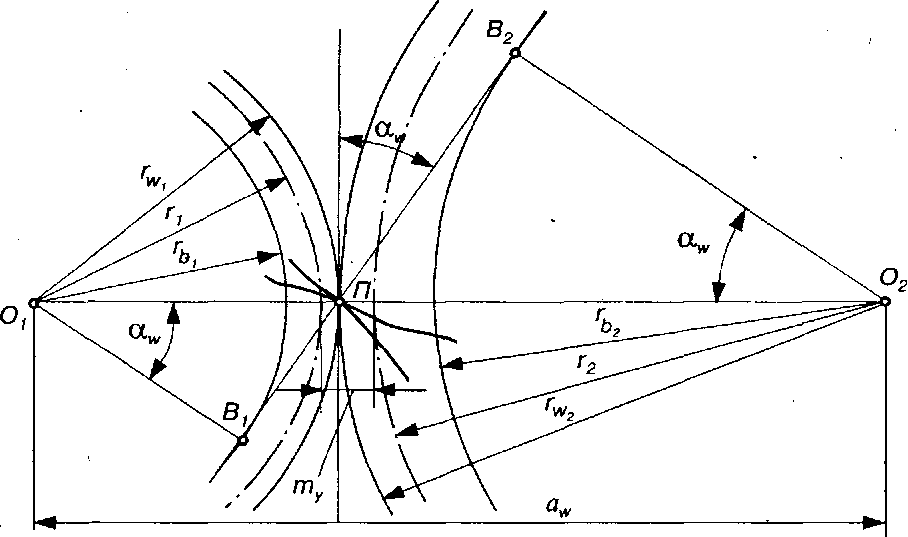
Рис. 9.19. До розрахунку геометричних параметрів прямозубої зубчастої передачі

Кутом зачеплення називають кут між лінією зачеплення В₁В₂ і прямою, що перпендикулярна до лінії центрів. Цей кут чисельно дорівнює куту профілю зубів кожного з коліс передачі у точці, що лежить на почат­ковому колі.

Маючи на увазі, що 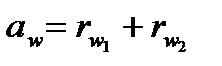, та враховуючи формули (9.6) і (9.32), запишемо:

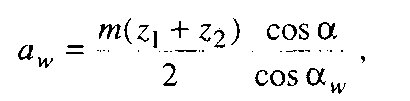
(9.34)

або

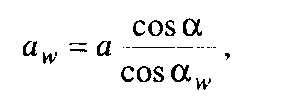
(9.35)

де

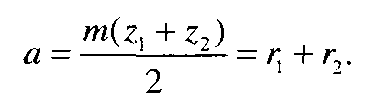
(9.36)

Тут а – ділильна міжосьова відстань, що дорівнює сумі радіусів ділильних кіл зубчастих коліс.

Різниця міжосьової і ділильної а відстаней називається сприймаль­ним (видимим) зміщенням і позначається

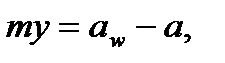(9.37)

де у – коефіцієнт сприймального зміщення, що виражається залежністю

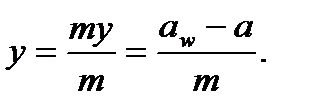(9.38)

На рис. 9.19 сприймальне зміщення ту визначається найменшою відстанню між ділильними колами. Зокрема, якщо х₁=х₂=0 або х₁= -х₂, то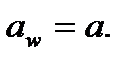

Виразами (9.34) або (9.35) можна скористатися лише після того, як буде знайдено кут зачеплення передачі за формулою [1, 5, 9]:

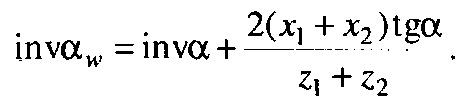
(9.39)

Діаметри кіл вершин, а значить, і висота ділильних головок, роз­раховуються за умови одержання бажаного радіального зазору с у зачеп­ленні зубчастих коліс. Стандарт не регламентує строго величину с. Най­більше розповсюдження одержали передачі, в яких радіальний зазор дорівнює с*т, де с* = 0,25.

Висота ділильних головок і радіуси кіл вершин визначаються відповідно за такими формулами:

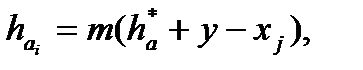(9.40)

де – коефіцієнт зміщення при нарізанні j-го зубчастого колеса; у – коефі­цієнт сприймального зміщення.

Отже, радіус кола вершин

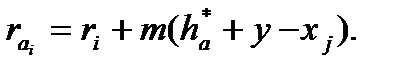(9.41)

У табл. 9.1 наведені формули для визначення основних геометричних параметрів прямозубої зубчастої передачі зовнішнього зачеплення.

Таблиця 9.1

Геометричні параметри циліндричних зубчастих передач

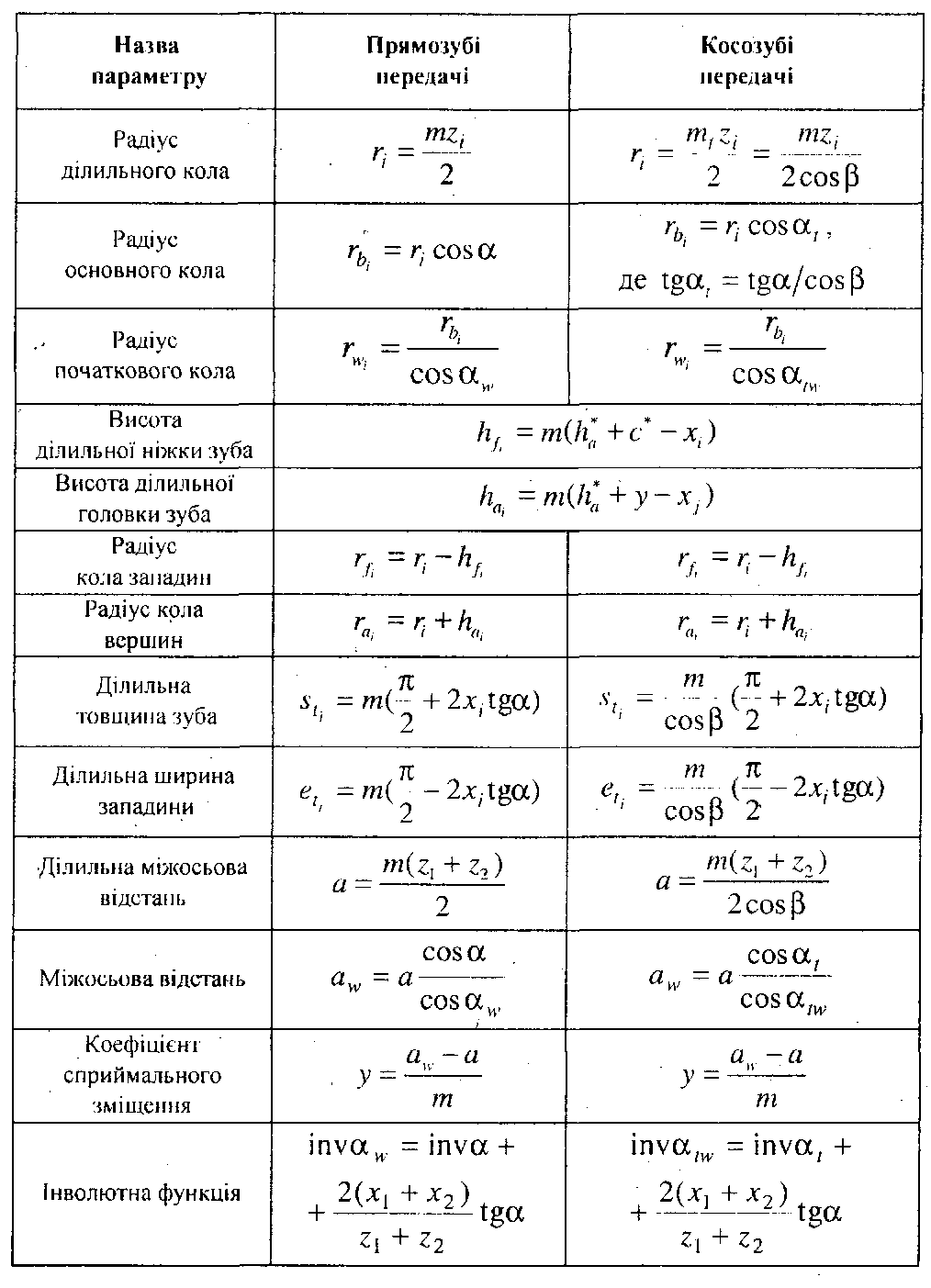
9.10. Особливості геометрії косозубих циліндричних передач

Раніше розглядались здебільшого зачеплення прямозубими цилін­дричними колесами. У таких передачах контакт між зубами проходить по прямій, паралельній до осей обертання, причому зуби одночасно по всій довжині входять у зачеплення й одночасно виходять із нього. Картина зачеплення в будь-якій площині, перпендикулярній до осі обертання коліс, однакова за геометрією і часом. Тому неточності, які завжди мають місце при виготовленні зубчастих коліс (наприклад, неточність профілю, неста­лість кроку та ін.), а також деформації і спрацювання деталей, погіршують їх роботу (збільшується шум, зменшується довговічність передачі тощо). Крім цього, плавність роботи у прямозубих передач порівняно невелика.

Для усунення вказаних недоліків, як уже зазначалось, на практиці часто використовують косозубі або шевронні циліндричні передачі (рис. 9.2, б, в). Бічну поверхню косого зуба утворює пряма АВ₁ поверхні N (рис. 9.20, а), яка обкочується без ковзання відносно основного циліндра радіуса 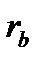. Пряма АВ₁ утворює з твірною АВ основного циліндра кут 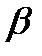. Цей кут називають кутом нахилу зубів. Кожна точка прямої АВ₁ описує таку ж евольвенту, як і точка А, утворюючи при цьому нециліндричну, а гвинтову лінійчату евольвентну поверхню зуба.

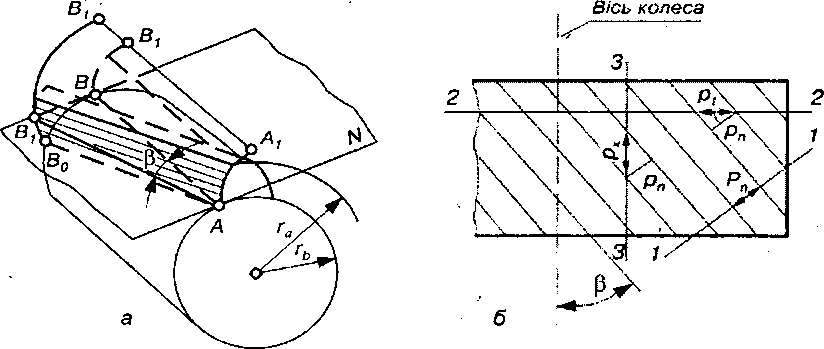
Рис 9.20. До геометрії косозубого колеса:

а) утворення евольвентного профілю зуба; б) твірна косозуба рейка

Картина зачеплення зубів у косозубій передачі в будь-якому пере­тині, як і в прямозубій передачі, однакова. Проте на відміну від прямозубої передачі зачеплення у всіх перетинах відбувається несинхронно в часі, тобто зуби входять у зачеплення не зразу по всій довжині, а поступово.

Косозубі циліндричні зубчасті колеса нарізаються рейками, лінії зубів яких складають з віссю колеса, що нарізається, кут 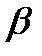. На рис. 9.20, б зображено план косозубої вихідної твірної рейки, на якій нанесені лінії зу­бів. При такому розташуванні ліній зубів їх крок можна вимірювати у трьох плоских перетинах рейки:

а) перетин 1-1, нормальний до теоретичної лінії зубів, у якому ви­мірюють нормальний крок р_n;

б) перетин 2-2, перпендикулярний до осі зубчастого колеса, що нарі­зається рейкою (торцевий перетин), у якому вимірюють торцевий крок p_t ;

в) перетин 3-3 (осьовий перетин) площиною, паралельною до осі зуб­частого колеса, що нарізається рейкою, в якому вимірюють осьовий крок р_х .

Контур зубчатої рейки в нормальному перетині і є тим вихідним твірним контуром, розміри якого залежать від розрахункового модуля т. Тому

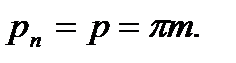(9.42)

З рис. 9.20, б легко одержати значення торцевого і осьового кроків зубів залежно від нормального:

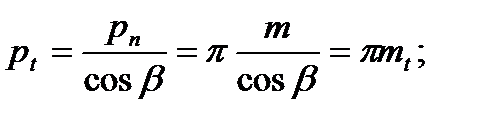(9.43)

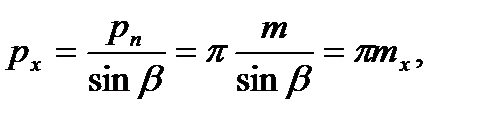(9.44)

де 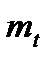і 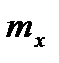– відповідно торцевий і осьовий модулі, які визначаються формулами:

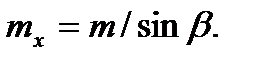(9.45)

Для розрахунку геометричних параметрів косозубих зубчастих коліс важливо визначити параметри торцевого контуру косозубої рейки, оскільки цей контур профілює евольвенту зубчастого колеса.

На рис. 9.21 накладено профі­лі зуба косозубої рейки в торцевому (контурна лінія) і нормальному (штри