Допустимі коефіцієнти нерівномірності руху деяких машин

Типи машин
Насоси	1/5 - 1/30
Сільськогосподарські машини	1/5-1/50
Металообробні верстати	1/20 - 1/50
Ткацькі, поліграфічні та мукомельні машини	1/10-1/50
Бавовнопрядильні машини	1/60-1/100
Суднові.двигуни	1/20-1/150
Двигуни внутрішнього згорання	1/80-1/100
Компресори	1/50-1/100
Електричні генератори Постійного струму	1/100-1/200
Електричні генератори змінного струму	1/200-1/300
Авіаційні двигуни, турбогенератори	1/200 і менше

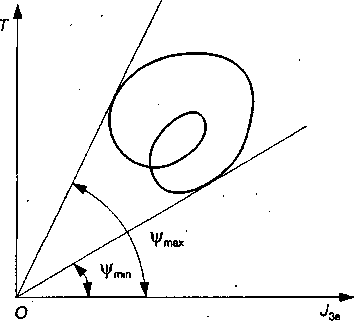
Визначення коефіцієнта нерівномірності руху машини за допомогою кривої Віттенбауера

Якщо побудовано діаг­раму 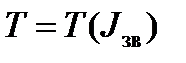, то неважко ви­значити значення коефіцієнта не­рівномірності руху під час устале­ного руху. На ділянці усталеного руху ця крива має бути замкне­ною, оскільки ті самі значення величин Т і 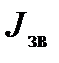періодично по­вторюються через кожний цикл. На рис. 5.2 зображено частину кривої 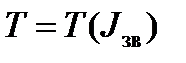, що відповідає періоду усталеного руху.

Рис. 5.2. Визначення коефіцієнта нерівномірності руху машини за допомогою кривої Віттенбауера

Для визначення коефіцієнта 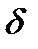необхідно мати значення максимальної 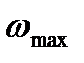і мінімальної 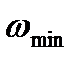швидкості ланки зведення (5.7). З формули (4.60) випливає, що максимальна кутова швидкість 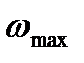за час усталеного руху відповідає максимальному значенню тангенсу кута 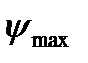(рис. 5.2), мінімальна кутова швидкість 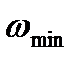відповідає значенню тангенсу кута .

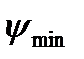Для визначення цих кутів проводимо з точки 0 до кривої 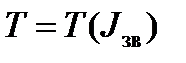дві дотичні: під найбільшим кутом 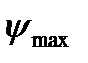і найменшим ку­том 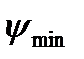. Тоді згідно з рівнянням (4.60) можна записати

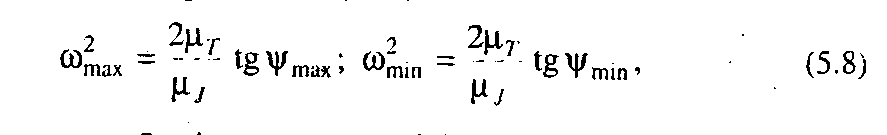
(5.8)

де 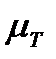, 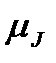– масштаби кінетичної енергії і зведеного моменту інерції.

Помноживши чисельник і знаменник правої частини формули (5.7) на 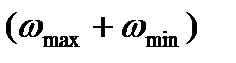, маємо

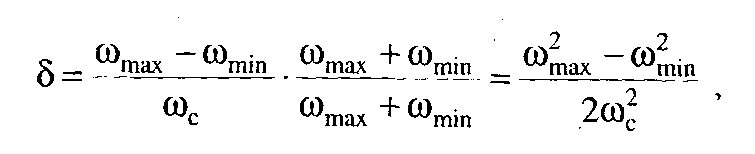
(5.9)

оскільки .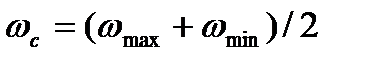

Підставляючи у формулу (5.9) вирази (5.8), дістанемо

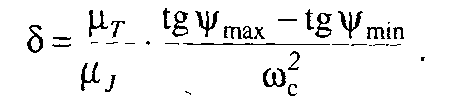(5.10)

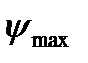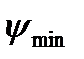Кути і визначаються безпосередньо з рисунка, а величина 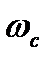– за формулами (5.5) або (5.6).

Коефіцієнт нерівномірності руху механізму або машини можна також визначити за діаграмою швидкостей, побудованою на рис. 4.14. Для цього знаходимо 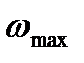і 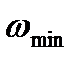для періоду усталеного руху та під­ставляємо їх значення у формулу (5.7).