Визначення моменту інерції маховика методом Віттенбауера

Як показано вище, за допомогою кривої Віттенбауера 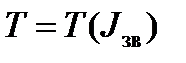для періоду усталеного руху можна визначити коефіцієнт нерівномірності руху механізму або машини. Тоді, очевидно, якщо при заданій зведеній масі та кінетичній енергії відома залежність між ними, тобто побудовано діаграму 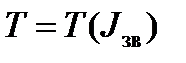, завжди можна з'ясувати питання, як мають бути змінені ці величини (зведений момент інерції 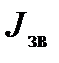і кінетична Т) для того, щоб забезпечити заданий коефіцієнт нерівно­мірності 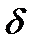. 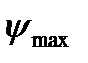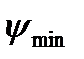Для розв'язання цієї задачі запишемо формули, які дозво­лять визначити значення кутів і (рис. 5.2), що відповідають заданим 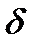8 і діаграмі .

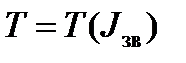Розв'язуючи рівняння (5.6) і (5.7) відносно 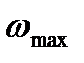і 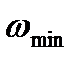, знаходимо:

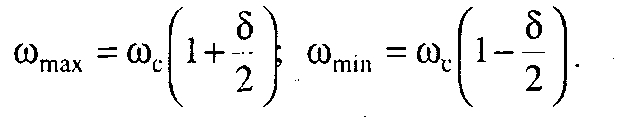
(5.11)

Підносячи праві і ліві частини цих рівнянь до квадрата, дістанемо:

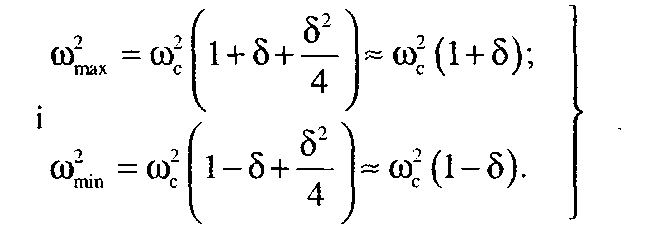
(5.12)

При малих значеннях коефіцієнтів 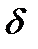членом 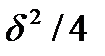можна знехтувати. Підставляючи в рівняння (5.12) вирази для 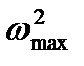і 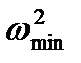з формул (5.8), після відповідних перетворень, дістанемо:

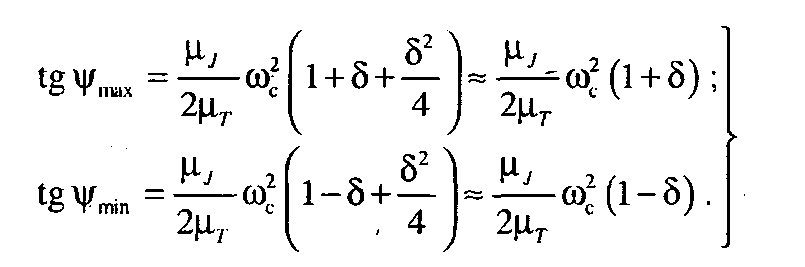
(5.13)

За допомогою рівнянь (5.13) можна для заданої кутової швид­кості 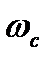і для будь-якого значення коефіцієнта нерівномірності руху 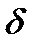визначити відповідні кути 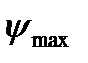і .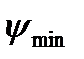

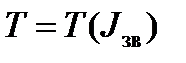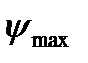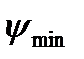Покажемо, як на практиці використати ці залежності. Нехай для деякого механізму або машини буде побудовано діаграму , яку в нашому випадку досить побудувати тільки для періоду усталеного руху (рис. 5.3). Провівши з початку координат 0 до кривої Віттенбауера дотичні під кутами і , знаходимо за формулою (5.10) коефіці­єнт нерівномірності руху механізму або машини.

Припустимо, що коефіцієнт 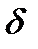буде більшим від допустимого значення 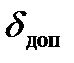для заданого типу машин. Тоді, підставивши в залеж­ність (5.13) замість 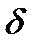допустиме його значення 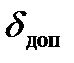, знаходимо зна­чення кутів 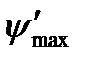і 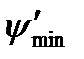, під якими проводимо дотичні до кривої Віттенбауера (рис. 5.3), і знаходимо їх точку перетину 0'. Очевидно, якщо б початок координат діаграми 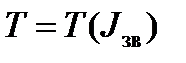знаходився у точці 0', то коефіцієнт нерівномірності 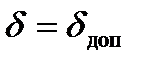. Тобто, якщо перейти від сис­теми координат 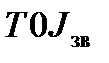до 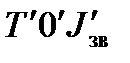, то задача про регулювання руху ме­ханізму або машини була б розв'язана. При цьому переході кінетична енергія збільшується на величину Т₀, а зведений момент інерції – на величину 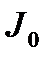. 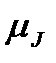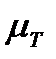Відрізки х і у, виміряні у міліметрах, зображують у вибраних масштабах і величини додаткового зведеного момен­ту інерції 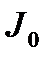і додаткової кінетичної енергії Т₀ , які необхідні для того, щоб машина працювала з вибраним коефіцієнтом нерівномірності 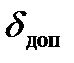.Отже,

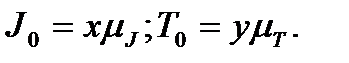(5.14)

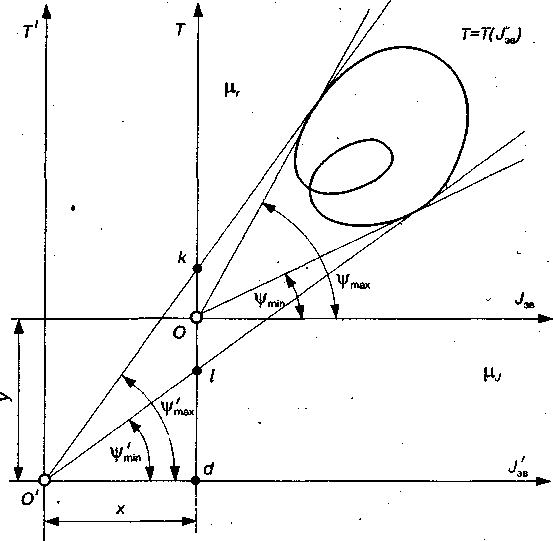
Рис. 5.3. Визначення моменту інерції маховика методом Віттенбауера

З побудови безпосередньо випливає, що чим менший коефіці­єнт нерівномірності 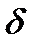, тим менша різниця між кутами 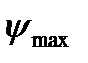і 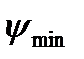, і тим далі від кривої 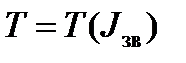, що відповідає часові усталеного руху, буде початок координат, тобто при зменшенні величини 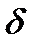зростає зве­дена маса машини і її кінетична енергія, потрібна для надання руху машині із заданою середньою швидкістю 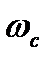. Отже, збільшення рівномірності руху ланки зведення можна досягти, збільшивши зведений момент інерції механізму чи машини. Збільшити зведені маси або зве­дений момент інерції можна за рахунок збільшення мас окремих ланок механізму. Практично це збільшення мас здійснюється за допомогою посадки на один з валів машини додаткової деталі, що має певний мо­мент інерції. Ця деталь називається маховим колесомабо маховиком. Як було показано вище, для того, щоб забезпечити заданий коефіцієнт нерівномірності 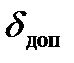, треба збільшити зведений момент інерції меха­нізму або машини на величину 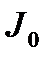(5.14). Величина цього додаткового моменту і визначає момент інерції маховика, тобто

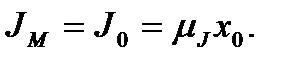(5.15)

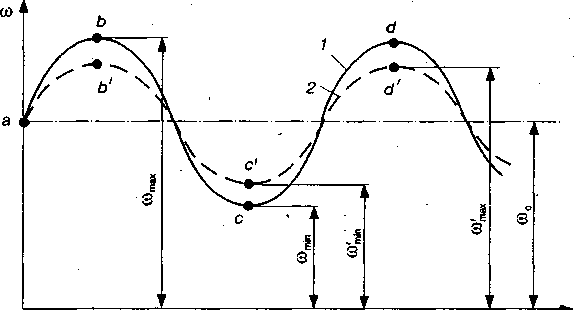
Завданням маховика є регулювання періодичних коливань швидкості початкової ланки, які обумовлені властивостями самих ме­ханізмів або періодичною зміною співвідношень між величинами ру­шійних сил і сил опору. Підбором моменту інерції маховика можна змусити початкову ланку механізму рухатись з наперед заданим відхи­ленням від деякої її середньої швидкості. Маховик є ніби акумулятором кінетичної енергії механізмів або машини, що нагромаджує її в момен­ти прискорення руху механізмів і віддає назад у моменти сповільнення руху машини. Для кращого розуміння дії маховика як гасителя коли­вань швидкості обертання тіла, біля його середнього значення на рис. 5.4 показано дві діаграми 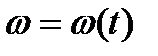: 1 - машини без маховика, 2 - ма­шини з маховиком. Введення маховика в машину дозволяє зменшити коливання швидкості відносно її середнього значення 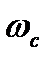, тому при збільшенні швидкості обертання ланки зведення (на рис. 5.5 ділянки ab, сd) частина кінетичної енергії машини йде на збільшення кінетич­ної енергії маховика ( 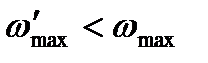), і, навпаки, коли швидкість обер­тання зменшується, маховик віддає частину нагромадженої кінетичної енергії машині, завдяки чому зміна швидкості буде менша 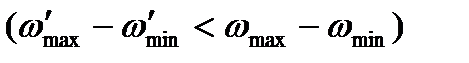. Крива 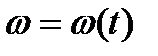попаде не в точку с, а в точку 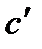.У деяких робочих машинах, в яких корисне навантаження періодично змінюється в значних межах (дробарки, прокатні стани і т.п.), маховик акумулює дуже значні запаси кінетичної енергії в мо­менти прискорення руху, тобто в моменти зниження корисних наван­тажень. Така акумулююча роль маховика дає можливість використати нагромаджену ним енергію для подолання підвищених корисних навантажень без збільшення потужності двигуна.

Рис. 5.4. Зменшення коливань швидкості за допомогою маховика

Для зменшення коливань швидкості маховик повинен мати відпо­відний момент інерції. Згідно з формулою (4.38) 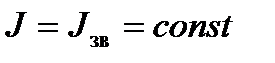, прийнявши 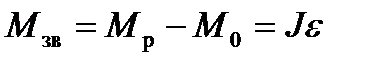маємо

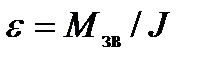. (5.16)

Отже, чим більший момент інерції 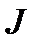обертових мас (вклю­чаючи маховик) при тому ж самому зведеному (надлишковому) момен­ті сил, тим менше кутове прискорення 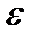ланки зведення, а значить, тим менша зміна кутової швидкості.

На основі того, що кутове прискорення 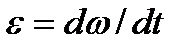, залежність (5.16) можна записати у такому вигляді:

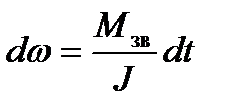. (5.17)

Звідси видно, що при всіх інших рівних умовах зміна величини кутової швидкості 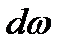прямо пропорційна часу дії надлишкового мо­менту М_зв. Це показує, що результуюча дія маховика найефективніша при короткочасних коливаннях величини обертового моменту М_зв, а також при різких (миттєвих) змінах величини опору. Маховик не допо­може, якщо, наприклад, при тому ж навантаженні на паровий двигун упаде тиск пари в котлі або при цьому ж тиску значно збільшилось на тривалий час навантаження. У таких випадках використовуються регулятори швидкості, мова про яких буде далі (п. 5.5).

Для більшої ефективності дії маховика, зменшення маси, габа­ритів доцільно його ставити на швидкохідний вал, оскільки кінетична енергія маховика, у результаті зміни якої здійснюється регулювання швидкості машини, виражається формулою:

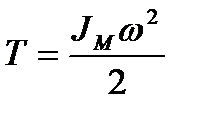(5.18)

Звідси видно, що ця енергія прямо пропорційна 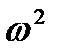. Цим дуже часто користуються на практиці, встановлюючи маховик на швидко­хідному валу, наприклад в інерційному стартері. Проте деколи маховик встановлюють і на тихохідних валах, ближче до тих частин машини (джерела коливання швидкості), нерівномірність руху яких треба зменшити, щоб ці коливання швидкості не передавались на інші ланки передавального механізму (зубчасті колеса, муфти тощо).

Якщо маховик встановлюється не на ланці зведення, а на будь-якій і-й ланці машини, то завжди повинна задовольнятися умова рів­ності кінетичної енергії:

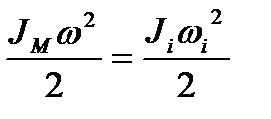, (5.19)

де 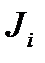– момент інерції маховика, встановленого на і-й ланці; 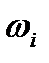– кутова швидкість цієї ланки.

З рівняння (5.19) випливає

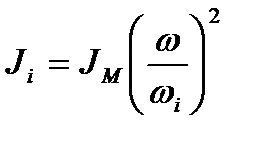. (5.20)

Отже, чим більшою буде кутова швидкість і-оїланки, тим менший повинен бути момент інерції маховика. Тому вигідно з точки зору зменшення ваги або діаметра маховика встановлювати його на ланках, що мають великі швидкості.

З рівняння (5.20) також випливає, що для забезпечення умови ста­лості моменту інерції 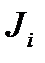необхідно, щоб передаточне відношення 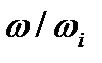було сталим, що вимагає встановлення маховика на ланках, які зв'язані з ведучим валом механізму передаточним відношенням сталої величини (механізми круглих зубчатих коліс, черв'ячні механізми і т. д.).

При встановленні маховика не на ланці зведення необхідно врахувати жорсткість проміжного кінематичного ланцюга При малій жорсткості кінематичного ланцюга пружні коливання можуть бути та­кими великими, що махове колесо не виконуватиме свого призначення.

Треба зазначити далі, що при малих значеннях коефіцієнта 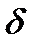внаслідок незначної різниці між кутами 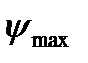і 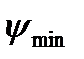точка перетину 0' дотичних (рис. 5.3) дуже часто знаходиться за межами рисунка. У цьому випадку можна використати точки перетину k і l дотичних з віссю Т першої системи координат. Тоді, очевидно:

.

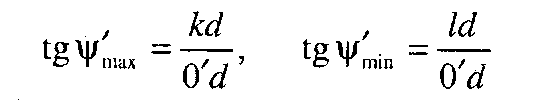
і, далі,

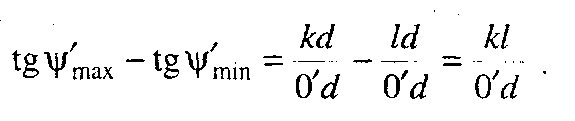
(5.21)

Підставляючи (5.21) у рівняння (5.10), знаходимо

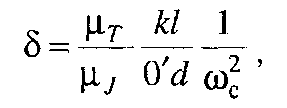
звідки, враховуючи, що 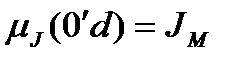, дістаємо

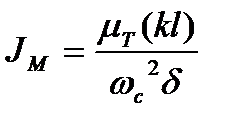(5.22)

Аналогічно можна дістати формулу для визначення моменту інерції маховика через точки перетину дотичних з віссю абсцис 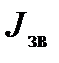першої системи координат.

Визначення розмірів маховика.Оскільки маховик звичайно роблять у вигляді колеса (рис. 5.5), що має масивний обід 1, сполуче­ний з втулкою 2 спицями 3 (або тонким диском), то моментами інерції з'єднуючих частин часто нехтують і наближено вважають, що маса маховика рівномірно розподілена по колу радіуса R = D/2, геометрич­ному місцю центрів ваги поперечних перерізів обода. Тоді момент інерції маховика можна виразити так:

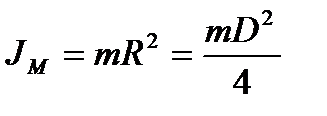(5.23)

де m - маса ободу маховика.

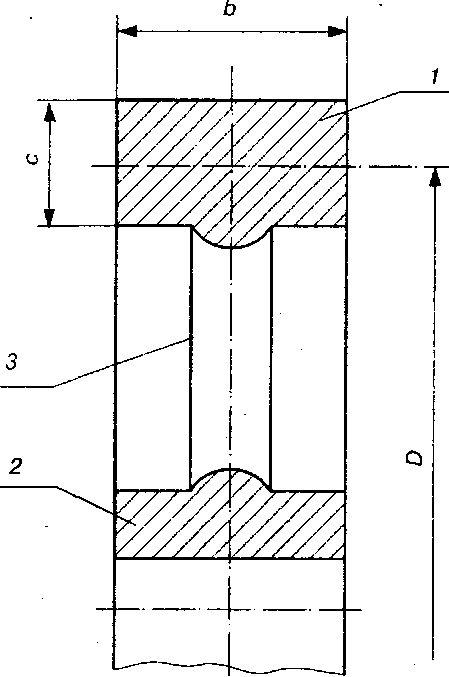
Рис. 5.5. Конструкція маховика

Добуток маси обода маховика на квадрат його діаметра тD² називається маховим моментом або характеристикою маховика. Для багатьох деталей машин, що здійснюють обертовий рух (муфти, ротори електродвигунів тощо) ця характеристика наводиться в довід­никах. Характеристика маховика має одиницю кг∙м². За нею легко ви­значити необхідну масу маховика, якщо задано або вибрано його діа­метр, значення якого визначається з чисто конструктивних міркувань Щоб запобігти небезпеці можливого розриву маховика, його діаметр D вибирають таким, щоб колова швидкість на ободі не перевищувала, допустимої для матеріалу маховика величини. Можна рекомендувати для перевірки діаметра маховика таку залежність:

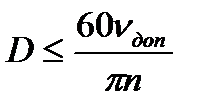, (5.24)

де 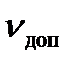– допустима колова швид­кість обода маховика, яка не повинна перевищувати для стальних маховиків 70-120 м/с, для чавунних - 30-45 м/с; п -частота обертання маховика, .

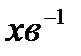Якщо врахувати, що маса ободу маховика може практично бу­ти прийнята

,

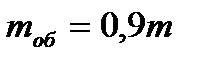де 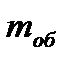– маса обода маховика, тоді ширина b обода маховика визначається з виразу

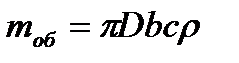. (5.25)

Tут 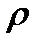– густина матеріалу ( ); .

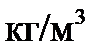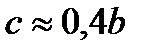Тоді, якщо прийняти 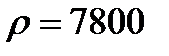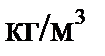, маємо

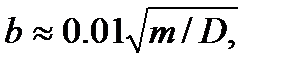(м). (5.26)

Наближений метод побудови кривої Віттенбауера.Отже, ма­ючи побудовану діаграму 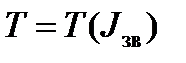при заданих коефіцієнті нерівно­мірності руху 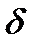і середній кутовій швидкості обертання 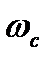ланки зве­дення, можна визначити момент інерції маховика і, тим самим, визначи­ти його масу й розміри. Проте на практиці ця задача ускладнюється тим, що для побудови діаграми 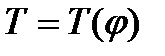необхідно мати діаграми зведених моментів рушійних сил 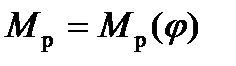і сил опору 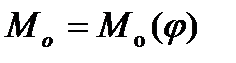. Причо­му для робочих машин, знаючи технологічні опори, можна знайти зна­чення зведених моментів сил опору (див. п. 4.6), тобто побудувати діаг­раму 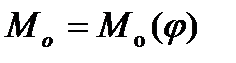. Приклад такої діаграми показаний на рис. 5.6,а. Зве­дений момент рушійних сил, як правило, для таких машин важко знайти, а тому його приймають сталим, тобто 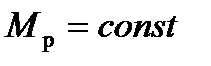, величину якого можна визначити, виходячи з рівності робіт рушійних сил 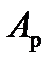і сил опору 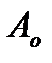за один цикл руху механізму або машини.

Діаграму роботи сил опору 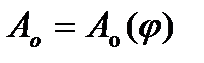можна одержати шля­хом графічного інтегрування діаграми 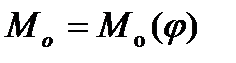(рис. 5.7, б), оскіль­ки робота визначається залежністю

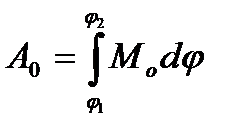(5.27)

Як відомо, графічна інтерпретація інтеграла є площа, яка об­межена кривою 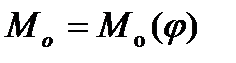, віссю 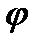і крайніми ординатами, ділянки кривої, що відповідають кутам 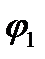і 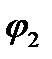. Наприклад, на ділянці а – 2 робота сил опору

;

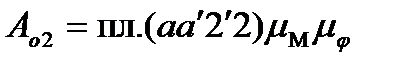на ділянці 2-3

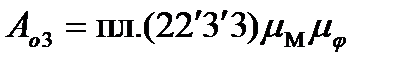і т.п.

Відклавши на відповідних ординатах ці роботи у масштабі 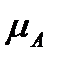, одержимо діаграму 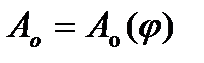. Практично цих розрахунків не роблять,

а виконують побудову, обернену до тої, яку ми робили при графічному диференціюванні (методом хорд). А саме: площу криволінійної трапе­ції 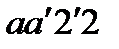замінюємо площею прямокутника, висоту якого переносимо на вісь координат 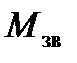, здобуту точку з'єднуємо з точкою Р. Відрі­зок 0Р=Н визначає масштаб побудови діаграми робіт

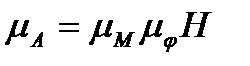. (5.28)

У нашому випадку робота сил опору на ділянці 0 – a дорівнює ну­лю, оскільки 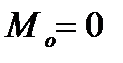. Тоді з точки а на діаграмі 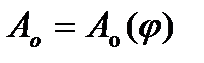(рис. 5.7, б) проводимо на ділянці a – 2 лінію 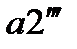, паралельну 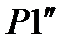і дістанемо точку 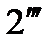. Аналогічно здійснюємо побудову на інших ділянках (2-3, 3-4 і т.п), що дозволяє здобути точки 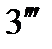, і т.д., з'єднавши які плавною кри­вою, дістанемо діаграму 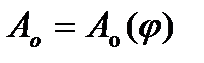. На ділянці 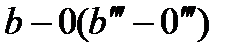робота 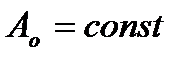, оскільки 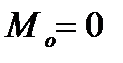, і робота сил опору не змінюється.

Діаграма робіт рушійних сил 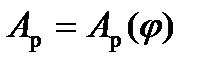при такому припу­щенні ( 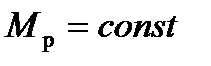) зображатиметься прямою лінією 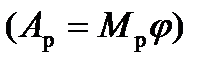, яка проходитиме через точки 0 і 0'" діаграми 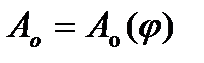. Це пояснюється тим, що зміна кінетичної енергії 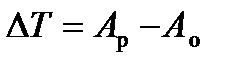, за один цикл усталеного руху дорівнює нулю, тобто на початку і в кінці циклу 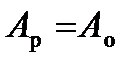. Про­вівши через точку Р лінію (рис. 5.6, а), яка паралельна лінії 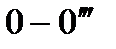на діаграмі робіт (рис. 5.6, б), дістанемо точку 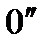, яка визначить величину зведеного моменту рушійних сил .

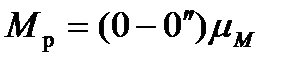На підставі діаграм робіт рушійних сил і сил опору будуємо ді­аграму зміни кінетичної енергії механізму або машини без маховика за формулою:

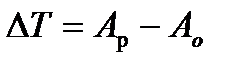. (5.29)

Якщо діаграма 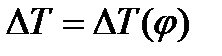будується в тому ж масштабі, що і діаграми робіт, досить на відповідних ординатах (рис. 5.6,в).відкласти відрізки, які знаходяться між кривими 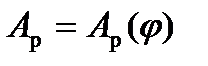і 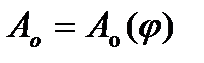, тоб­то 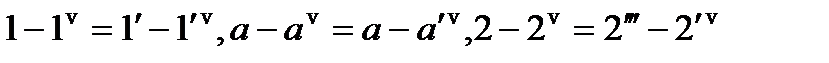і т.д. Якщ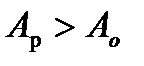о , то 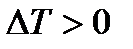, і навпаки, якщ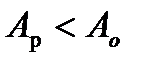о , то .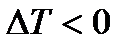

Діаграми зведених моментів інерції 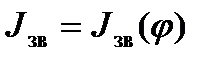(рис. 5.7,г) і крива Віттенбауера 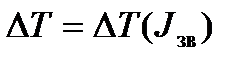(рис. 5.6,д) будується так, як це описано вище (п. 4.7, 4.12).

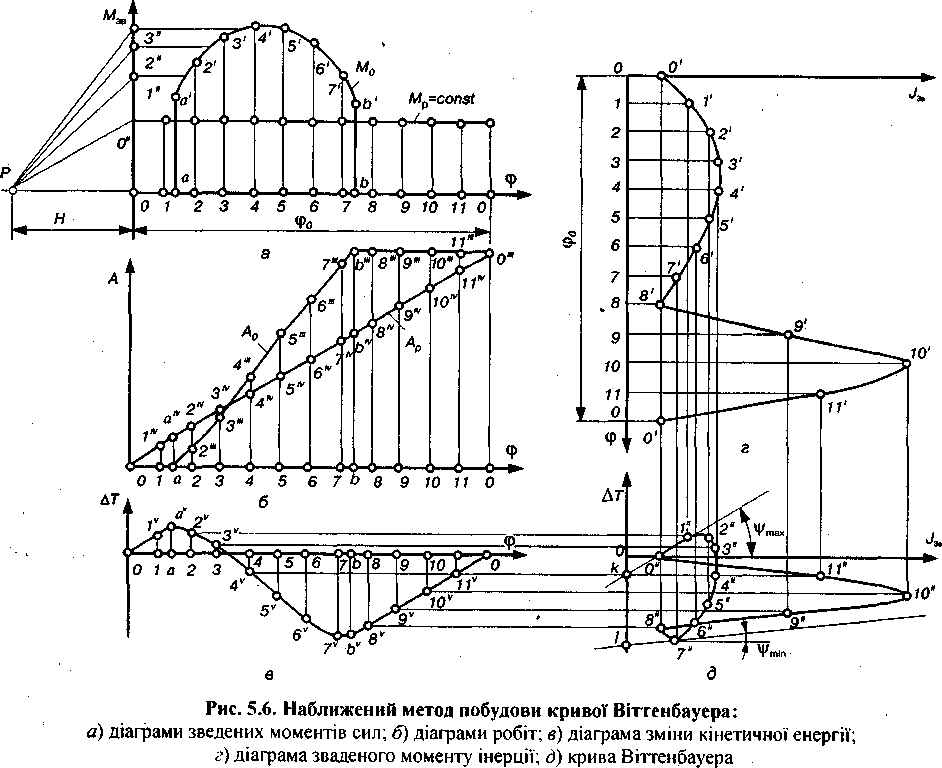
Рис. 5.6. Наближений метод побудови кривої Віттенбауера:

а) діаграма зведених моментів сил; б) діаграми робіт; в) діаграма зміни кінетичної енергії; г) діаграма зведеного моменту інерції; д) крива Віттенбауера.

Для машини-двигуна, як правило, неважко побудувати діаг­рами зведених рушійних сил 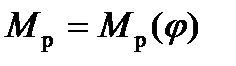маючи індикаторну діагра­му, тобто знаючи тиск p на робочий поршень залежно від переміщення поршня s. Тоді методом графічного інтегрування цієї діаграми будує­мо діаграму робіт рушійних сил 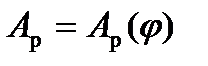. У таких машинах зведений момент сил опору приймається сталим 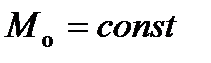. Всі інші побудови виконуються аналогічно.

У технічній і навчальній літературі наводяться інші методи ви­значення моменту інерції маховика. Заслуговують на особливу увагу методи, які враховують механічні характеристики двигунів.