Примеры некоторых распределений

Элементы математической статистики. Основные понятия

Математическая статистика – это раздел теории вероятностей. Занимается она сбором и обработкой опытных данных, т.е. прикладными задачами теории вероятностей.

Как уже отмечалось в §2, частота появления случайного события стремится к вероятности этого события, если число испытаний неограниченно растет. Поэтому на практике, когда вероятность неизвестна, ее заменяют на частоту, получаемую экспериментально. Говорят, что частота р^* является оценкой вероятности р, т.е. ее приближенным значением.

Основной задачей математической статистики является оценка закона распределения случайной величины или числовых характеристик, если в законе распределения нет необходимости.

Пусть при неоднократном измерении некоторой случайной (или неслучайной) величины мы получили серию из n результатов (x₁, x₂, …, x_n). В силу неизбежных случайных ошибок измерения не все результаты измерений одной и той же величины будут совпадать друг с другом.

Очевидно, любое измерение x_i можно считать оценкой измеряемой величины, если она неслучайная, или оценкой ее математического ожидания, если это случайная величина x. Однако, интуитивно ясно, что среднее арифметическое n измерений

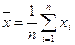(1)

будет более точной оценкой математического ожидания m_x случайной величины x. Среднее арифметическое 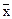обычно и берут в качестве оценки математического ожидания, т.е. m_x» .

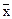Оценкой начальных моментов k-го порядка a_k[x] служат соответствующие статистические моменты , т.е.

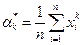a_k[x]» . (2)

Оценкой центральных моментов m_k[x] служат соответствующие статистические центральные моменты 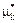, т.е. m_k[x]» 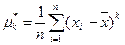. (3)

Если известно математическое ожидание m_x, то в качестве оценки m_k[x] лучше взять величину

. (4)

Определение. Статистической функцией распределения F^*(x) случайной величины x называют частоту события (x<x), т.е.

F^*(x)=Р^*(x<x), (5)

где Р^*(x<x) - частота события (x<x).

Чтобы найти значение F^*(x), нужно подсчитать число испытаний (измерений), в которых величина x принимает значение меньшее х, и разделить это число на общее число испытаний n.

Аналитически статистическую функцию распределения можно записать так

F^*(x) , (5¢)

где h(х) – функция Хевисайда.

Очевидно, и для дискретной, и для непрерывной случайной величины x функция F^*(x) будет ступенчатой, разрывной в точках x_i. Все свойства функции распределения F(x) справедливы и для статистической функции распределения F^*(x). Поскольку частота события (x<x) стремится к вероятности этого события, то естественно в качестве оценки функции F(x) взять функцию F^*(x).

Повторим серию независимых измерений случайной величины x и, в силу случайных ошибок, вместо прежней серии измерений (x₁, x₂, …, x_n) получим новую (x₁’, x₂’, …, x_n’). Отсюда ясно, что серию измерений (x₁, x₂, …, x_n)=х можно рассматривать как случайный вектор, а его координаты x_i как случайные величины, имеющие тот же закон распределения, что и измеряемая случайная величина x. Ясно также, что все статистические моменты являются величинами случайными. При оценке числовых характеристик мы заменяем точные значения на случайные величины. Указать предельную погрешность, которую мы совершаем при этом, мы не можем, т.к. она не имеет смысла. Однако методы статистики, которые мы рассмотрим позже, позволяют найти вероятность такой погрешности.

Случайный вектор х=(x₁, x₂, …, x_n) называют выборкой из генеральной совокупности. Под генеральной совокупностью понимают всю бесконечную мыслимую совокупность измерений. Приведем другой пример. Пусть необходимо узнать средний бюджет жителей Таганрога. Для этого придется опросить всех жителей города. Они и представляют собой генеральную совокупность. Т.к. опросить всех жителей города задача трудоемкая и дорогостоящая, то делают случайную выборку, т.е. опрашивают только некоторую часть жителей города, но результат опроса распространяется на всех. Ясно, что результаты эти будут случайными.

Обработать выборку можно различными способами. Если измерения x_i упорядочить по величине, расположив в порядке неубывания, то полученную выборку называют вариационным рядом. Разность R=x_max-x_min называется размахом выборки. Если в вариационном ряде оставить только различные измерения, но указать их частоту повторения, то получим статистический ряд.

Если объем выборки велик, то весь интервал выборки разбивают на несколько разрядов. Подсчитывают число измерений, попавших в каждый разряд, вычисляют частоту каждого разряда, т.е. отношение числа измерений в разряде к числу всех измерений выборки, и все это сводят в таблицу, которая называется группированным статистическим рядом.

Результаты группированного статистического ряда можно использовать для построения гистограммы. Она строится следующим образом. По оси ОХ откладывают длины разрядов и над каждым разрядом строят прямоугольник, площадь которого равна частоте разряда. Так что суммарная площадь прямоугольников равна единице. Полученную диаграмму и называют гистограммой.

Пример. При измерении заряда электрона Милликеном было получено 58 измерений (в 10^-10 абс. эл. стат. единицах) 4,781; 4,795; 4,764; 4,769; 4,792; 4,792; 4,779; 4,764; 4,795; 4,775,… (ради упрощения мы привели только десять из этих измерений). Построить: 1) статистический ряд распределения; 2) статистическую функцию распределения; 3) группированный статистический ряд; 4) гистограмму; 5) найти средний заряд электрона и среднее значение квадрата ошибки измерений.

Решение. 1). Все 58 измерений есть выборка, приведенные 10 измерений – также выборка. Статистический ряд построим для десяти измерений.

Xi	4,764	4,769	4,775	4,779	4,781	4,792	4,795

2) Статистическую функцию построим также для десяти измерений (см. рис. 11).

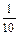
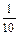
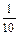
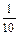
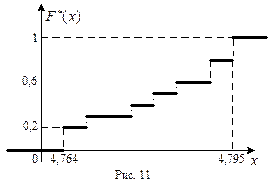
3) В случае 58 измерений размах выборки R=4,810-4,740=0,07. Разобьем весь этот диапазон значений на 7 равных разрядов, подсчитаем частоту каждого разряда и получим следующий группированный статистический ряд:

Разряды	4,74-4,75	4,75- 4,76	4,76-4,77	4,77-4,78	4,78-4,79	4,79-4,80	4,80-4,81
Частота

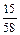
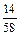
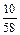
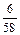
4) Ширина каждого из семи прямоугольников в гистограмме равна 0,01, а высоты равны соответствующей частоте, умноженной на 100 (см. рис. 12).

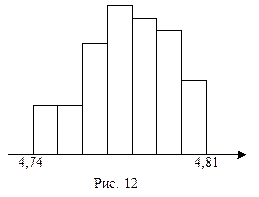
5) Для оценки заряда электрона воспользуемся формулой (1).

При n=10 получим 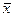=4,7807, а при n=58 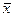=4,7808.

Для оценки квадрата ошибки измерений воспользуемся формулой (3) при k = 2, только n заменим в ней на (n – 1). Причина этого будет ясна позже. При n = 10 получим 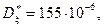а при n = 58

Примеры некоторых распределений

1. Биномиальное распределение. Дискретная случайная величина ξ с конечным числом возможных значений x_k=k=0,1,2,…,n называется распределенной по биномиальному закону, если соответствующие вероятности даются формулой Бернулли

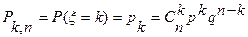. (1)

По биномиальному закону распределено, например, число успехов в n испытаниях Бернулли (см §7.). Воспользуемся биномом Ньютона

. (2)

Из (2) видно, что формула (1)- это k-й член разложения бинома Ньютона. Отсюда и название распределения. Из этой же формулы (2) видно, что .

Найдем математическое ожидание.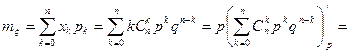

.

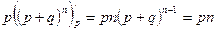(Индекс внизу означает, что производная берется по p).

Итак, 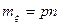. (3)

Для вычисления дисперсии воспользуемся формулой

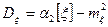. (4)

Продифференцируем (2) по p два раза и умножим полученное равенство на p². В результате получим

,

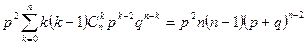или ,

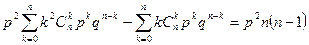или . (5)

Подставляя из (5) в (4), найдем с учетом (3)

. (6)

Можно доказать, что мода М₀ случайной величины ξ, распределенной по биномиальному закону, удовлетворяет условию

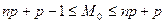. (7)

В частности, если 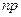число натуральное, то оно и является модой. Коэффициент асимметрии определяется формулой

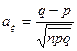. (8)

1. Геометрическое распределение. Дискретная случайная величина ξ, возможными значениями которой является бесконечная последовательность натуральных чисел 1,2,3,…, а соответствующие вероятности даются формулой

, (9)

называется распределенной по геометрическому закону. Если число испытаний Бернулли не ограничивать, а проводить их до первого успеха, то число всех испытаний (вплоть до первого успеха) есть случайная величина ξ, распределенная по геометрическому закону. Название закона обязано тому, что вероятности (9) образуют геометрическую прогрессию со знаменателем q.

Проверим условие 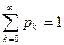. Действительно,

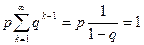. (10)

Найдем математическое ожидание

.

Итак, 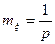. (11)

Для нахождения дисперсии вычислим сначала . Из (10) получим . Продифференцировав последнее тождество два раза по q и умножив обе части полученного равенства на q, найдем

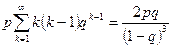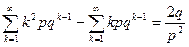, или

, или

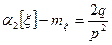. (12)

Подставляя из (12) в (4) и учитывая (11), получим

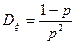. (13)

Пример 1. Сколько в среднем расходуется патронов, чтобы поразить цель, если вероятность попадания p=0,2, а цель поражается при первом же попадании?

Решение. Воспользуемся (11), получим 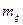=5.

2. Распределение Пуассона. Дискретная случайная величина ξ, возможными значениями которой являются члены последовательности 0,1,2,…, а соответствующие вероятности даются формулой

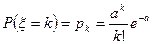, (14)

называется распределенной по закону Пуассона, – параметр.

В §7 доказано, что закон Пуассона является предельным для биномиального, его называют законом редких явлений. По закону Пуассона может быть распределено, например, число телефонных звонков, поступивших на телефонную станцию за некоторый промежуток времени.

Убедимся, что 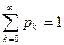. Действительно,

.

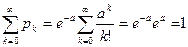Найдем математическое ожидание

= = .

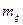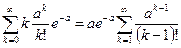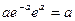Итак, 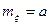. (15)

Чтобы найти дисперсию, вычислим предварительно второй начальный момент .

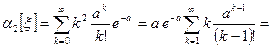
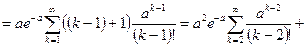
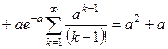. (16)

Подставляя (16) и (15) в (4), найдем

. (17)

Таким образом, при распределении Пуассона .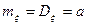

Пример 2. Среднее число отказов аппаратуры за год равно 3. Определить вероятность отказа аппаратуры в течение месяца.

Решение. Очевидно, 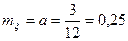. Пусть событие А означает нуль отказов за месяц. Тогда согласно (14) . Событие 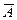означает отказ аппаратуры (хотя бы один отказ). .

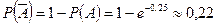3. Равномерное распределение. Если все возможные значения непрерывной случайной величины ξ лежат в

конечном интервале (α, β), а плотность вероятности постоянная на этом интервале (см. рис. 13), то говорят, что случайная величина ξ распределена равномерно (см.§9). Плотность распределения можно записать так

.

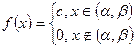Постоянную с найдем, используя свойство плотности распределения 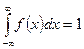. В нашем случае . Найдем математическое ожидание

. (18)

Аналогично найдем дисперсию

(19)

Из (18) видно, что кривая распределения симметрична относительно центра распределения, поэтому все центральные моменты нечетного порядка обращаются в нуль. Медиана совпадает с .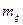

Пример 3. Автобусы ходят с интервалом 5 минут. Найти вероятность того, что случайно подошедший к остановке пассажир будет ожидать автобус не более 3-х минут.

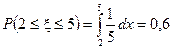Решение. (см. рис. 14).

4. Показательный закон. Непрерывная случайная величина распределена по показательному закону, если ее плотность имеет вид

λ>0 – параметр (см. рис. 15). Найдем функцию распределения

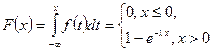
(см. рис .16).

Найдем математическое ожидание . Интегрируя по частям, получим

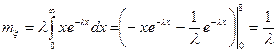. (20)

Найдем дисперсию

.

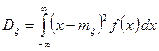После двукратного интегрирования по частям получим

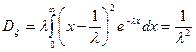. (21)

Коэффициент асимметрии 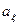и медиана определяются формулами

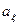=2, . (22)

Упражнение. Проверить условие 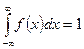и формулы (22).

Время безотказной работы многих электронных приборов подчиняется показательному закону.

Пример 4. Определить вероятность того, что аппаратура безотказно проработает не менее 3-х лет, если ее среднее время безотказной работы 2 года.

Решение. По условию задачи , .

.

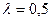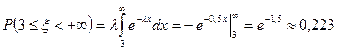5. Гамма-распределение. Этот закон распределения является обобщением показательного. Плотность гамма - распределения определяется формулой

(23)

Параметры a и l могут быть любыми положительными числами, 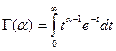- гамма – функция (см. §1 гл.4). При a=1 гамма-распределение совпадает с показательным распределением.

Используя свойства гамма – функции, найдем математическое ожидание и дисперсию.

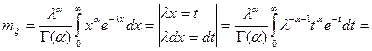
. Итак,

. (24)

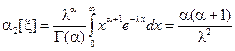, (25)

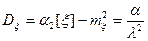. (26)

Мода М₀ и коэффициент асимметрии 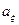определяются формулами

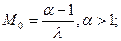
. (27)

Распределение хи-квадрат с n степенями свободы является частным случаем гамма – распределения. Плотность этого распределения определяется формулой (23) при l=0,5, a=0,5n. Числовые характеристики также получаются по соответствующим формулам (24-27) при l=0,5, a=0,5n.

По закону хи-квадрат с n степенями свободы распределена, например, сумма n квадратов случайных величин ξ_i, подчиненных некоторым дополнительным условиям.

6. Нормальное распределение. Если плотность распределения непрерывной случайной величины ξ определяется формулой

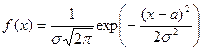, (28)

то говорят, что случайная величина распределена по нормальному закону (по закону Гаусса) с параметрами и σ. Обозначают N( ,σ). Если 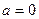, 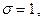то закон называется стандартным нормальным и обозначается N(0,1).

Нормальный закон распределения играет исключительную роль в теории вероятностей. Исключительное положение этого закона объясняется тем, что он является предельным законом, к которому стремятся многие другие законы распределения. Это утверждение носит название центральной предельной теоремы, с которой мы познакомимся позже.

Кривая распределения (28) симметрична относительно точки х= . При изменении параметра кривая смещается вдоль оси Ох, не меняя своего вида. В точке х= кривая достигает своего максимума . При уменьшении σ величина 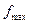увеличивается, а т.к. площадь, ограниченная кривой распределения, остается равной единице, то кривая сжимается с уменьшением σ. Точки х= ±σ являются ее точками перегиба, ось Ох – асимптотой. Найдем математическое ожидание.

.

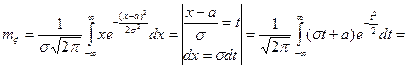
Воспользовались интегралом Пуассона

,

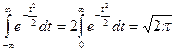а первое слагаемое обращается в нуль, т.к. подынтегральная функция нечетная. Итак,

m_ξ= (29)

Очевидно, математическое ожидание, мода и медиана совпадают. Найдем центральные моменты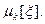

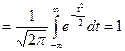. Тем самым мы проверили основное свойство плотности распределения. Первый центральный момент 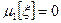для любого распределения, поэтому найдем 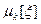при k≥2.

. Итак,

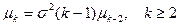. (30)

Из (30) найдем 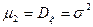, т.е. параметр есть среднее квадратичное отклонение. Из равенства 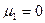и (30) следует, что все центральные моменты нечетного порядка обращаются в нуль. Легко проверить, что эксцесс 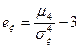для нормального распределения равен нулю. Все другие кривые распределения сравнивают с кривой нормального распределения. Если 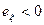, то кривая распределения более плосковершинная по сравнению с гауссовой кривой, при - более островершинная.

Неэлементарная функция , определенная несобственным интегралом

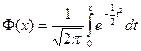, (31)

называется интегралом вероятности. Выразим функцию распределения F(x) через интеграл вероятности.

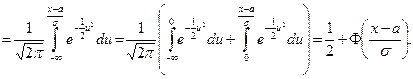
Итак, 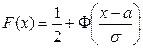. (32)

Из (32) получим

.(33)

Пример 5.Найти вероятность события 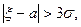если случайная величина 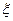распределена нормально.

Решение. Р(|ξ- |>3σ)=1-Р(|ξ- |≤3σ)=1-Р( -3σ≤ξ≤ +3σ) = =1-Ф(3)+Ф(-3)=1-2Ф(3)=1-2·0,49865=0,0027. Значение Ф(3) взято из таблиц.

Таким образом, для нормально распределенной величины все ее практически возможные значения ограничены интервалом (m_ξ-3σ_ξ, m_ξ+3σ_ξ), а событие оказывается практически невозможным. Этот факт носит название “правила трех сигма”.