Оценка регрессии по выборке
Пусть закон распределения случайной величины (ξ,η) неизвестен. Проведем над случайной величиной n независимых испытаний (измерений), получим выборку 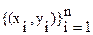 . Ее можно обработать следующим образом. Расположим величины xi в строку таблицы в порядке возрастания x1<x2<…<xk, считая все значения один раз. Аналогично значения yi расположим в порядке возрастания y1<y2<…<ym в столбец таблицы. Подсчитаем, сколько раз повторяется пара значений
. Ее можно обработать следующим образом. Расположим величины xi в строку таблицы в порядке возрастания x1<x2<…<xk, считая все значения один раз. Аналогично значения yi расположим в порядке возрастания y1<y2<…<ym в столбец таблицы. Подсчитаем, сколько раз повторяется пара значений 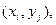 разделим это число на число всех измерений n, получим частоту
разделим это число на число всех измерений n, получим частоту 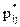 . Эту частоту поставим на пересечении i-го столбца и j-ой строки таблицы. В результате получим статистическую таблицу, аналогичную таблице распределения, приведенной в §14. Эту статистическую таблицу возьмем в качестве оценки закона распределения случайной величины (ξ,η).
. Эту частоту поставим на пересечении i-го столбца и j-ой строки таблицы. В результате получим статистическую таблицу, аналогичную таблице распределения, приведенной в §14. Эту статистическую таблицу возьмем в качестве оценки закона распределения случайной величины (ξ,η).
Суммируя частоты 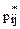 по столбцам (по индексу i), получим статистический ряд распределения для компоненты η. Суммируя
по столбцам (по индексу i), получим статистический ряд распределения для компоненты η. Суммируя 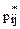 по индексу j, получим статистический ряд распределения для компоненты ξ. Имея эти статистические распределения, можно найти условные частоты:
по индексу j, получим статистический ряд распределения для компоненты ξ. Имея эти статистические распределения, можно найти условные частоты:
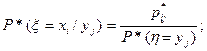
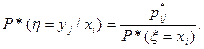
Эти формулы аналогичны формулам (6,7) §15. Зная условные частоты, можно найти оценку условного математического ожидания M*[η/xi] по формуле, аналогичной формуле (6) §18. Только вероятность в ней следует заменить на частоту.
Нанесем в декартовой системе координат точки (xi,M*[η/xi]), i=1,2,…,k. Если провести среднюю линию по этим точкам, то полученную линию g*(x) можно взять за оценку регрессии η на ξ. Аналогично можно поступить с точками (M*[ξ/yj],yj), j=1,2,…,m и получить оценку регрессии ξ на η.
Найдем теперь аналитическое выражение для оценки регрессии g*(x). По виду кривой g*(x) можно сделать предположение (гипотезу) о характере зависимости: линейная g*(x)=ax+b, квадратичная g*(x)=ax2+bx+c и пр. Неизвестные параметры a,b,c можно найти из условия минимума величины δ, определяемой формулой:
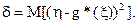 (1)
(1)
(Сравним с (5) §18). Рассмотрим подробнее случай линейной функции g*(x)=ax+b. Преобразуем выражение (1) к виду M[(η-aξ-b)2]=Ф(a,b) и, учитывая, что математическое ожидание от суммы равно сумме математических ожиданий (это утверждение мы докажем позже), найдем
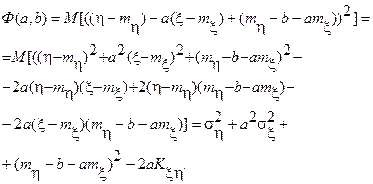
Необходимыми условиями минимума функции Ф(a,b) являются равенства 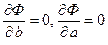 . Это приводит к системе:
. Это приводит к системе:
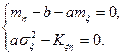 (2)
(2)
Решая систему (2), найдем 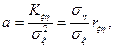
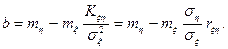 Можно доказать, что функция Ф(a,b) действительно достигает минимума. Таким образом мы нашли аналитическое выражение для оценки линейной регрессии
Можно доказать, что функция Ф(a,b) действительно достигает минимума. Таким образом мы нашли аналитическое выражение для оценки линейной регрессии
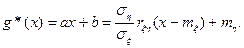 (3)
(3)
Функцию (3) называют линейной средней квадратичной регрессией η на ξ. Аналогично можно получить среднюю квадратичную регрессию ξ на η:
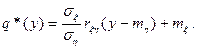 (4)
(4)
Коэффициенты 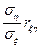 и
и 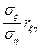 называются коэффициентами регрессии.
называются коэффициентами регрессии.
Если все случайные величины центрированы, то из (3) получим:
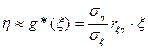 . (5)
. (5)
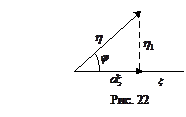 Дадим геометрическую интерпретацию. Спроектируем вектор η (случайную величину η) на вектор ξ. Очевидно, что
Дадим геометрическую интерпретацию. Спроектируем вектор η (случайную величину η) на вектор ξ. Очевидно, что
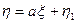 (6)
(6)
(см. рис. 22).
Умножим (6) скалярно на ξ (см. §17), получим 
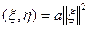 , или
, или
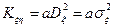 , или
, или 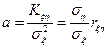 . (7)
. (7)
Перепишем (6) с учетом (7):
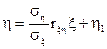 . (6¢)
. (6¢)
Сравнивая (6¢) с (5), видим, что линейная регрессия ξ на η есть проекция ξ на η. Величина η1 в (6) характеризует ошибку при замене η на g*(ξ).
Если теоретические числовые характеристики, входящие в линейные регрессии (3,4) неизвестны, то их заменяют на соответствующие статистические числовые характеристики. В результате получают эмпирические линейные регрессии. Статистические характеристики получают по соответствующим формулам теоретических характеристик, заменяя в них вероятность на частоту.
Аналогично поступают при нахождении нелинейной регрессии.
Дата добавления: 2020-02-05; просмотров: 611;











