Понятие о критериях согласия

Обрабатывая независимые измерения случайной величины ξ, мы можем построить статистическую функцию распределения F^*(x). По виду этой функции можно принять гипотезу, что истинная теоретическая функция распределения есть F(x). Сами независимые измерения (x₁, x₂,…,x_n), образующие выборку, можно рассматривать как одинаково распределенные случайные величины с гипотетической функцией распределения F(x).

Очевидно, между функциями F^*(x) и F(x) будут некоторые расхождения. Возникает вопрос – являются ли эти расхождения следствием ограниченности объема выборки или связаны с тем, что наша гипотеза не верна, т.е. действительная функция распределения не F(x), а какая-то другая. Для решения этого вопроса пользуются критериями согласия, суть которых в следующем. Выбирается некоторая величина Δ(F, F^*), которая характеризует степень расхождения между функциями F^*(x) и F(x). Например, Δ(F, F^*)=Sup|F(x)-F^*(x)|, т.е. верхняя грань по х модуля разности.

Считая гипотезу верной, т.е. зная функцию распределения F(x), можно найти закон распределения случайной величины Δ(F, F^*) (вопроса, как это сделать, мы касаться не будем). Зададим число р₀ столь малое, что осуществление события {Δ(F, F^*)>Δ₀}с этой вероятностью будем считать практически невозможным. Из условия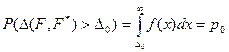

найдем величину Δ₀. Здесь f(x) – плотность распределения Δ(F,F^*).

Вычислим теперь величину Δ(F, F^*)= Δ₁ по результатам

выборки, т.е. най­дем одно из возможных значений случайной величины Δ(F, F^*). Если Δ₁≥Δ₀, то это означает, что произошло практически невозможное событие. Объяснить это можно тем, что наша гипотеза не верна. Итак, если Δ₁≥Δ₀, то гипотеза отвергается, а при Δ₁<Δ₀, гипотеза может оказаться неверной, но вероятность этого мала.

В качестве меры расхождения Δ(F, F^*) можно брать различные величины. В зависимости от этого получаются различные критерии согласия. Например, критерий согласия Колмогорова, Мизеса, Пирсона, или критерий хи-квадрат.

Пусть результаты n измерений оформлены в виде группированного статистического ряда с k разрядами.

РАЗРЯД (x₀,x₁) [x₁,x₂) … [x_k-1,x_k)

ЧАСТОТА р₁^* р₂^* … р_k^*

Зная функцию распределения F(x), найдем вероятность р_i того, что случайная величина ξ попала в i-тый разряд. За меру расхождения Δ(F, F^*) возьмем величину

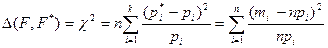. (1)

Здесь - число измерений в i-том разряде. Пирсоном доказано, что закон распределения случайной величины (1) стремится к закону распределения хи-квадрат с (k-1) степенью свободы при неограниченном увеличении объема выборки. Поэтому при больших n можно использовать этот закон (см. §12 пр.6). Получаются хорошие результаты, если np_i≥10.

Замечание. Если в гипотетической функции распределения неизвестные параметры заменяются их оценками, полученными из выборки определенными методами, то число степеней свободы в распределении хи-квадрат уменьшается на число оцененных параметров.

Пример. В §11 мы построили группированный статистический ряд для измеренной величины заряда электрона. Выскажем гипотезу, что измеренные величины распределены равномерно на отрезке [α, β] (фактически мы предполагаем, что ошибки измерения распределены равномерно на некотором отрезке). Тогда вероятность попадания в каждый из семи разрядов будет равна 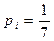. Используя группированный ряд из §11, вычислим Δ(F, F^*)= Δ₁= по формуле (1). В данном случае .

.

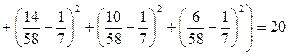Поскольку в гипотетический закон распределения входят два неизвестных параметра, α и β – начало и конец отрезка, то число степеней свободы будет 7-1-2=4. По таблице распределения хи-квадрат при выбранной вероятности p₀=10^-3 найдем Δ₀=18. Т.к. Δ₁>Δ₀, то гипотезу о равномерном распределении ошибки измерения придется отбросить.