Числовые характеристики многомерной случайной величины
Основными числовыми характеристиками двумерной случайной величины (ξ,h) являются начальные и центральные моменты.
Определение 1. Начальным моментом αks порядка (k+s) случайной величины (ξ,h) называют число, определяемое формулой

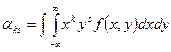 . (1)
. (1)
Здесь f(x,y) - плотность распределения случайного вектора (ξ,h).
Очевидно, α00=1. Наиболее употребительными являются начальные моменты α10 и α01.
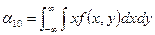 =
= 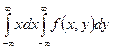 =
=
= 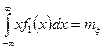
Аналогично найдем, что α01=mη. Точку (mξ,mη) называют центром распределения величины (ξ,h).
Определение 2. Центральным моментом mks порядка (k+s) случайной величины (ξ,h) называют число, определяемое формулой:
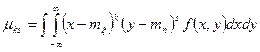 . (2)
. (2)
Поскольку μ01= μ10=0, то наиболее употребительными являются центральные моменты второго порядка μ20, μ02, μ11.
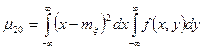 =
= 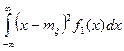 =
= 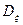 .
.
Аналогично найдем, что μ02=Dη; Dξ и Dη – дисперсии компонент ξ и h. Они характеризуют рассеяние случайного вектора (ξ,h) в направлениях осей координат x и y.
Особую роль играет второй смешанный момент μ11:
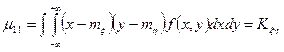 . (3)
. (3)
Его называют корреляционным моментом. Формулу (3)можно преобразовать к виду:
Кξη=α11 – mξmη. (3¢)
Если случайная величина (ξ,h) дискретная с конечным числом возможных значений, то формулы (1), (2), (3¢) удобнее писать в виде:
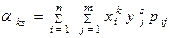 , (1¢)
, (1¢)
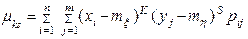 , (2¢)
, (2¢)
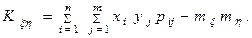 (3¢)
(3¢)
Теорема.Если ξ и η независимые, то корреляционный момент равен нулю, kξη=μ11=0.
Доказательство. Если ξ и η независимые, то f(x,y)=f1(x)f2(y). Тогда
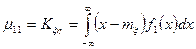
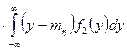 = 0.
= 0.
Теорема доказана.
Определение 3. Если корреляционный момент Кξη равен нулю, то ξ и η называются некоррелированными. Если Кξη¹0 - то они называются коррелированными.
Следствие. Коррелированные величины являются зависимыми.
Доказательство. От противного. Пусть они независимые. Тогда согласно теореме Кξη=0, что противоречит условию. Следствие доказано.
Замечание. Обратное утверждение неверно, т.е. зависимые случайные величины могут быть некоррелированными, а некоррелированные - зависимыми.
Из теоремы и следствия ясно, что корреляционный момент Кξη характеризует не только рассеяние случайного вектора (ξ,h), но и в какой-то степени зависимость между величинами ξ и h. Для оценки степени этой зависимости вводят понятие коэффициента корреляции:
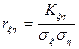 . (4)
. (4)
Можно доказать, что 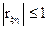 . При этом, если rξη=0, то величина ξ и η некоррелированные, если
. При этом, если rξη=0, то величина ξ и η некоррелированные, если 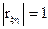 , то они связаны линейной функциональной зависимостью. Таким образом, чем ближе модуль коэффициента корреляции к единице, тем теснее линейная связь между компонентами ξ и η.
, то они связаны линейной функциональной зависимостью. Таким образом, чем ближе модуль коэффициента корреляции к единице, тем теснее линейная связь между компонентами ξ и η.
Аналогично определяются числовые характеристики n-мерного случайного вектора ξ=(ξ1, ξ2,…,ξn). В частности:
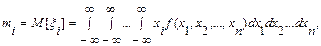 (5)
(5)
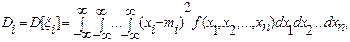 (6)
(6)
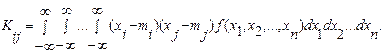 (7)
(7)
Из (7) видно, что Kij=Kji, Kii=Di.
Корреляционные моменты Kij образуют корреляционную матрицу. Матрица симметричная, по главной ее диагонали стоят дисперсии компонент вектора.
Пример. Найти корреляционный момент Kξη случайного вектора пр.1 §14.
Решение. В пр.1 §14 найдены ряды распределения компонент ξ и η. Воспользуемся ими и найдем mξ и mη:
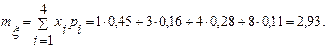
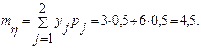
Согласно (3//):
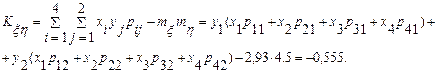
Итак, Kξη=-0.555, следовательно, компоненты ξ и η зависимые.
Дата добавления: 2020-02-05; просмотров: 694;











