Независимость случайных величин. Условные законы распределения
В §5 были введены понятия независимых и зависимых случайных событий. Аналогичные понятия вводятся и для случайных величин.
Пусть случайные величины ξ1,ξ2,…,ξn заданы на некотором вероятностном пространстве (Ω, 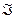 ,P). Случайные величины ξ1,ξ2,…,ξn называются независимыми в совокупности (или просто независимыми), если имеет место равенство
,P). Случайные величины ξ1,ξ2,…,ξn называются независимыми в совокупности (или просто независимыми), если имеет место равенство 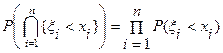
 (1)
(1)
для произвольных x1, x2,…,xn. Если равенство (1) переписать в виде:
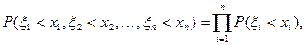
то легко перейти к терминам функции распределения
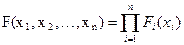 . (1¢)
. (1¢)
Здесь F(x1, x2,…,xn) - функция распределения случайного вектора ξ=(ξ1, ξ2,…,ξn), а Fi(xi) - функция распределения i-ой компоненты вектора ξ.
Теорема. Пусть f(x1, x2,…,xn) - плотность распределения случайного вектора ξ=(ξ1, ξ2,…,ξn). Случайные величины ξ1, ξ2,…,ξn независимы тогда и только тогда, когда во всех точках непрерывности функций f(x1, x2,…,xn), fi(xi), i=1,2,…,n имеет место равенство
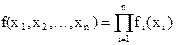 (2)
(2)
(без доказательства).
Здесь fi(xi) - плотность распределения i-ой компоненты вектора ξ.
Естественно, если условие (1¢) или (2) не выполняется, то случайные величины ξ1, ξ2,…,ξn зависимые. Однако, речь идет не о функциональной, а о так называемой вероятностной зависимости. Например, количество выпавших осадков и урожай - величины случайные. Интуитивно ясно, что они зависимые, но эта зависимость не функциональная. В предельном случае вероятностная зависимость может перейти в функциональную.
Если случайные величины зависимые, то функция распределения (плотность), например, первой компоненты вектора будет зависеть от того, какие значения приняли остальные компоненты вектора. Такую функцию распределения (плотность) называют условной и говорят об условном законе распределения.
Рассмотрим двумерный случайный вектор (ξ,h). Тогда F1(x/y) - условная функция распределения компоненты ξ при условии, что вторая компонента h приняла значение y. Аналогично определяются F2(y/x), f1(x/y), f2(y/x). Условные функция и плотность распределения обладают всеми свойствами безусловных функций и плотности распределения.
Можно доказать, что если ξ и h зависимые, то вместо (1¢) и (2) справедливы следующие формулы:
F(x,y)=F1(x)F2(y/x)= F2(y)F1(x/y), (3)
f(x,y)=f1(x)f2(y/x)= f2(y)f1(x/y). (4)
Равенства (3) и (4) называют теоремой умножения законов распределения. Из формул (1¢)-(4) следует, что условие независимости случайных величин ξ и h можно записать в виде:
F1(x/y)=F1(x), F2(y/x)=F2(y),
f1(x/y)=f1(x), f2(y/x)=f2(y). (5)
Для дискретной случайной величины (ξ,h) условные вероятности даются формулами:
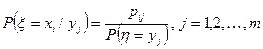 , (6)
, (6)
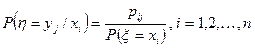 . (7)
. (7)
Пример 1. Найти закон распределения компоненты ξ случайного вектора (ξ,h), если а) h=y1=3,
б) h=y2=6 (см. пр.1 §14)
Решение: т.к. P(h=3)=0,5 и P(h=6)=0,5, то согласно (6) получим:
а) P(ξ =xi/3)= pi1/0,5; б) P(ξ =xi/6)= pi2/0.5, i=1,2,3,4. Условными законами распределения являются таблицы:
| а) | xi | ||||
| pi | 0,30 | 0,12 | 0,50 | 0,08 | |
| б) | xi | ||||
| pi | 0,6 | 0,2 | 0,06 | 0,14 |
Пример 2.Cлучайный вектор (ξ,h) задан своей плотностью f(x,y)= 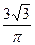 exp(–4(x-2)2–6xy–9y2). Найти условную плотность компонент ξ и h. Зависимы ли ξ и h ?
exp(–4(x-2)2–6xy–9y2). Найти условную плотность компонент ξ и h. Зависимы ли ξ и h ?
Решение: Плотности распределения ξ и h - f 1(x) и f 2(y) найдены в пр.2 §14. Из (4) найдем:
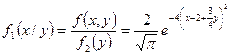 ,
,
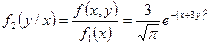 .
.
Поскольку f1(x/y)¹f1(x), то ξ и h зависимые.
Дата добавления: 2020-02-05; просмотров: 774;











