П.2. Метод Ньютона (касательных)

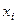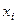Это итерационный метод нахождения корней нелинейного уравнения f (x) = 0. Геометрическая интерпретация одной итерации метода заключается в том, что в качестве корня уравнения принимается точка пересечения оси (Ох) и касательной, проведенной в точке ( , y( )), где 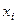- начальное приближение, к графику функции.

Пусть функция f (x) непрерывна на отрезке [a, b] и дважды непрерывно дифференцируема на интервале (a, b). Пусть корень x* 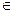[a, b] так, что f (a) · f (b) < 0. Положим x₀ = b. Проведем касательную к графику функции y = f(x) в точке B₀ = (x₀, f (x₀)).

Уравнение касательной будет иметь вид: y – f(x₀) = f ′(x₀)(x – x₀). Отсюда выразим х: . (*)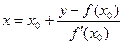

Первое приближение к решению получим, взяв абсциссу точки пересечения этой касательной с осью (Ох), т. е. положив в (*) y = 0, x = x₁: 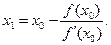Если f (х₁) = 0, то x₁ – искомый корень.

Если 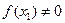, то проведем перпендикуляр к оси (Ох) х = х₁ до пересечения с графиком функции. Получим точку B₁(x₁, f (x₁)). Проведем касательную к графику функции y = f(x) в точке B₁(x₁, f (x₁)). Получим второе приближение, взяв абсциссу точки пересечения этой касательной с осью (Ох), т. е. положив в (*) y = 0, x = x₂: 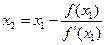. Если f (х₂) = 0, то x₂ – искомый корень.

Если 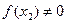, то процесс построения касательных продолжается. Аналогично как с точкой B₁, поступим с точкой B₂(x₂, f (x₂)), затем с точкой B₃(x₃, f (x₃)), и так далее, в результате получим последовательность приближений x₁, x₂, …, x_n, …, причем

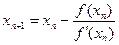- расчетная формула метода Ньютона. (**)

Сходимость метода Ньютона зависит от того, насколько близко к корню выбрано начальное приближение. Неудачный выбор начального приближения может дать расходящуюся последовательность.

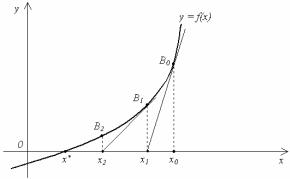
Теорема (Достаточное условие сходимости метода). Пусть [a, b] – отрезок, содержащий корень. Если в качестве начального приближения x₀ выбрать тот из концов отрезка, для которого f (x) · f "(x) ≥ 0, то итерации (**) сходятся, причем монотонно.

Рисунок соответствует случаю, когда в качестве начального приближения был выбран правый конец отрезка: x₀ = b.

Погрешность метода. На практике удобно пользоваться следующей апостериорной оценкой погрешности: | x_n – x*| ≤ | x_n – x_{n – 1}|.

Критерий окончания. Данная оценка позволяет сформулировать следующий критерий окончания итераций метода Ньютона. При заданной точности 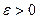вычисления нужно вести до тех пор, пока не будет выполнено неравенство | x_n – x_{n – 1}| .

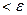Пример. Решим методом Ньютона уравнение x³+2x²+3x+5=0, взяв в качестве начального приближения 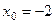и задав точность 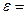0,000001.

Решение.

Поскольку 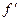(x)=3x²+4x+3, то итерационная формула метода Ньютона будет такой:

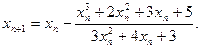
Применяя эту формулу, последовательно находим:

x₁ = -1,857143; критерий окончания не выполнен, так как | x_n – x_{n – 1}| = | -1,857143 – (-2)| .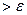

x₂ = -1,843842; критерий окончания не выполнен, так как | x_n – x_{n – 1}| = | -1,843842-(-1,857143)|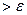

x₃ = -1,843734; | x_n – x_{n – 1}| = | -1,857143-(-1,843734)| 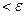, следовательно, критерий окончания выполнен.

x₄ = -1,843734.

Таким образом, x ≈ -1,843734 с точностью 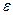. Как мы видим, значение корня с нужной нам точностью было получено уже на третьем шаге. (Четвёртый шаг понадобился для того, чтобы можно было убедиться, что с нужной нам точностью значение перестало изменяться.)

Вычисления удобно оформлять в виде таблицы.