Численные методы решения нелинейных уравнений

Уравнение с одним неизвестным можно записать в виде .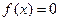

Уравнение нелинейное, если 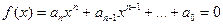, где .

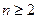Норвежский математик Абель доказал, что при 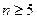не существует формулы, выражающей решение данного уравнения при помощи арифметических операций и извлечения корней. (Есть частные случаи). Кроме того, коэффициенты некоторых уравнений являются приближенными числами и, следовательно, вопрос о нахождении точных корней уравнения вообще не возникает. Поэтому большое значение приобретают численные методы.

Задача нахождения корней уравнения считается решенной, если корни вычислены с заданной степенью точности:‌ | ξ – x^* |‌‌‌‌‌‌‌‌‌‌‌‌^‌ < ε, где ξ – точный корень уравнения, х* – его приближенное значение, ε – точность.

Дано нелинейное уравнение с одним неизвестным f(x)=0. Процесс нахождения корней разбивается на два этапа. Первый - отделение корней, второй - уточнение корней до заданной степени точности.

Отделение корней.

Отделить корни - это значит разбить область допустимых значений на отрезки, в каждом из которых уравнение имеет один корень. Существует два метода отделения: графический и аналитический.

Первым методом по построенному графику функции определяют данные отрезки.

Для отделения корней по аналитическому методу необходимо: найти производную от функции y = f(x); найти стационарные 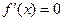и критические точки 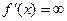функции и составить таблицу, в которой рассмотреть поведение производной и функции; разбить полученную область значений на более мелкие промежутки и найти интервалы, в которых содержаться корни уравнения.

Аналитический метод основан на теореме Больцано-Коши: если функция y = f(x) непрерывна на отрезке [а,b] и принимает на его концах значения разных знаков, то внутри отрезка содержится по крайней мере один корень уравнения f(x) = 0, то есть существует такая точка с из отрезка [а,b], что f(c) = 0.

Уточнение корней.

Для уточнения корней существуют несколько методов, например, метод проб, половинного деления, метод хорд, метод касательных (Ньютона).