П.1 Метод половинного деления

Пусть корни уравнения f(x)=0 отделены, т.е. известно, что уравнение имеет единственное решение х* на отрезке [а,b]. Следовательно, функция y=f(x) непрерывна и монотонна на отрезке [а,b] и принимает на его концах значения разных знаков: f(a)∙ f(b) < 0. Делим данный отрезок пополам. Получим точку с₀. Если f(c₀)=0, то с₀ – корень уравнения. Если нет, выбираем из отрезков [а, с₀] и [с₀,b] тот, на котором функция имеет значения разных знаков: f(a) ∙ f(с₀) < 0 или f(с₀) ∙ f(b) < 0. И выполняем аналогичные действия.

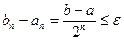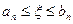Процесс деления отрезка пополам продолжается до тех пор, пока на некотором n-ом этапе либо середина отрезка станет корнем уравнения, либо найдется такой отрезок [a_n, b_n] , что и , где n – количество разбиений, а_n и b_n – корни уравнения с точностью до ε , ξ – точный корень уравнения. За приближенное значение корня х* следует взять 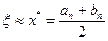. Погрешность .

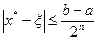Пример. Найти корни уравнения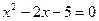

Решение.

Отделим корни аналитическим методом. Найдем стационарные точк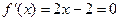и: при 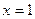. Составим таблицу, в которой рассмотрим поведение производной и функции:

x	-∞; 1		1; +∞
Знак	-		+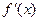
Поведение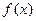

Разобьем полученную область значений на более мелкие промежутки и найдем интервалы, в которых содержаться корни уравнения.

х	-∞				+∞
Знак	+	-	-	-	+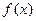

Уравнение имеет два корня (второй порядок - х²), происходит две перемены знака. Составим новую таблицу с более мелкими интервалами корня:

х	-5	-4	-3	-2	-1
Знак	+	+	+	+	-	-	-	-	-	+	+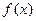

Из таблицы видно, что корни уравнения заключены в промежутках (-2; -1) и (3; 4).

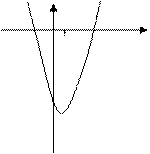
Замечание. Можно было отделить корни графическим методом: 1) построить графики функций 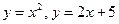и найти интервалы по х, где они пересекаются или 2) построить сразу график параболы .

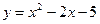Уточним корни методом половинного деления. Удобно все вычисления занести в таблицу.

Найдем корень х₁ на отрезке (-2, -1).

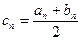
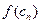
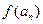
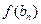
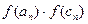
n	an-	bn+					знак	знак
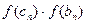
	-2	-1	-1,5	0,25		-2	+	-
	-1,5	-1	-1,25	-0,9375	0,25	-2	-	+
	-1,5	-1,25	-1,375	-0,359	0,25	-0,9	-	+
	-1,5	-1,375	-1,4375	-0,05859

Видим, что 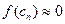при 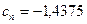. Следовательно, корень найден.

Погрешностьнайденного корня = .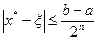

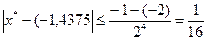Ответ:первый корень уравнения х₁ = -1,4375. Второй корень ищем аналогично.