Линейного программирования.
1. Метод простейших аппроксимаций (метод Фогеля)
На практике при решении задач в матрицах большого размера точные методы чрезвычайно трудоёмки, поэтому были разработаны более простые, обеспечивающие оптимальное или близкое к нему решение.
Из всего множества существующих приближ. методов метод простейших аппроксимаций является наиболее точным, так как в большинстве случаев он обеспечивает нахождение оптимального плана. Данный метод позволяет сопоставлять показатели однотипных технических средств на различных участках работ и различных технических средств на одном участке работ, т. е. сопоставление показателей производится как по строкам, так и по столбцам матрицы, что и обеспечивает оптимальное или близкое к нему решение. Данный метод может быть использован для широкого круга задач, в т. ч. для решения транспортной задачи.
Рассмотрим алгоритм метода простейших аппроксимаций на примере расстановки кранов на причалах.
Дано: m – количество типов кранов.
i = 1 ÷ m – индекс типа крана.
n – количество грузовых причалов.
j = 1 ÷ n – индекс причала.
ki – количество кранов каждого типа, имеющееся в порту.
Qj – навигационный грузооборот на каждом j – ом причале
(тыс. тонн)
Рij – производительность i- ого типа крана при работе на
j – ом причале, тысяч тонн за навигацию.
Необходимо расставить перегрузочные механизмы (краны) так, чтобы выполнить заданный грузооборот на каждом причале min – ым количеством кранов.
Искомая переменная.
Kij – это количество кранов i – ого типа, работающих на j – ом причале.
Z = 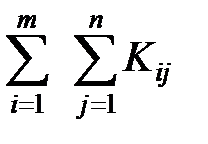 → min
→ min
Ограничения:
1) Kij ≥ 0
2) 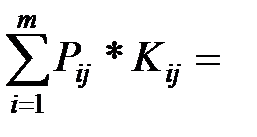 Qj
Qj
3) 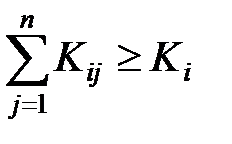
m = 5 k1 = 4, k2 = 7, k3 = 2, k4 = 3, k5 = 10
n = 5
Q1 = 600, Q2 = 2890, Q3 = 1100, Q4 = 2500, Q5 = 300
i
Pij = 
j
Алгоритм решения.
1)Необходимо расписать целевую функцию и ограничения с данными параметрами.
Z = k11 + k12 + k13 + k14 + k15 +
k21 + k22 ……………… +
k31 + k32………………. → min
1. 170k11 + 180k21 + 130k31 + 200k41 + 150k51 = 600
2. 380*k12 + 380*k22 + 200*k32 + ………. = 2890
3. = 1100
4. = 2500
5. = 300
6. k11 + k12 + k13 + k14 + k15 ≤ 4
7. k21 + k22 + k23 + k24 + k25 ≤ 7
8. ≤ 2
9. ≤ 3
10. ≤ 10
11. Kij ≥ 0
2) Представим исходные данные в виде матрицы, в которой будем осуществлять решение задачи.
| j | |||||||||||||||||
| i | Qj Кi | Столбцы разности | |||||||||||||||
| 3,5кр-1330 2)380 | 0,5кр-40 8)80 | | |||||||||||||||
| 3,35кр 6)180 | 1,55кр-400 5)260 | 2,1кр-189 7)90 | | | |||||||||||||
| 1кр 9)70 | |||||||||||||||||
| 3кр-1560 1)520 | | ||||||||||||||||
| 3,25кр 3)340 | 6,75кр-2100 4)310 | 100 | 130 | | |||||||||||||
| Строки разности. | |||||||||||||||||
| | |||||||||||||||||
3) В каждой строке и столбце матрицы определяется разность между двумя лучшими показателями (здесь между max производительностями) и заносятся значения разностей в строку (столбец) «разности».
После определения разностей выбираем наибольшую величину разности. При этом не имеет значения, где она находится: в строке или столбце.
Против выбранной max разности ставим перегруз. машины на тот причал, где достигается max производительность(в эту клетку ставится max количество кранов)
4) После постановки кранов на причал в таблице вычёркивается строка или столбец с заполненным квадратом. Строка вычёркивается, если расставлены все краны соответствующего типа; столбец – если выполнен заданный грузооборот.
Далее снова определяется разность 2-х лучших показателей в оставшихся строках и столбцах матрицы. Новые значения размещаются в следующей строке и столбце разности. Действие данного алгоритма повторяется до тех пор, пока не будет выполнен грузооборот на всех причалах или не будут расставлены все краны.
В результате решения получилось, что весь грузооборот можно выполнить без использования 1-ого крана 3-его типа. Необходимо рассчитать значение целевой функции для полученного плана и проверить ограничения.
| Z |
= 3, 5 + 0, 5 +
3, 35 + 1, 55 + 2, 1 +
1 +
3, 25 + 6, 75 =
Ограничения:
3, 35*180 = 600
3, 5*380 + 3*520 = 2890
3, 25*340 = 1100
1, 55*260 + 6, 75*310 = 2500
0, 5*80 + 2, 1*90 + 1*70 = 300
3, 5 + 0, 5 = 4
3, 35 + 1, 55 + 2, 1 = 7
1 < 2
3 = 3
3, 25 + 6, 75 = 10
Метод аппроксимации часто применяется для составления исходного плана в матрицах большого размера. Для получения строго оптимального плана необходимо приближённое решение закончить точным методом линейного программирования.
Сравнительный показатель трудоёмкости данного приближённого метода и любого точного метода составляет ≈ 50 единиц.
Дата добавления: 2019-12-09; просмотров: 937;











