Механизм единичного жребия.

Имитационное моделирование является методом математического описания стохастических (вероятностных) систем.

Имитационная модель представляет собой компьютерный аналог сложного реального явления и позволяет заменить эксперимент над реальной системой экспериментом с ее математической моделью на компьютере. Имитационное моделирование как метод исследования относится к классу численных методов, т. е. результат моделирования представляется в виде численных значений величин, оценивающих эффективность данной системы при заданных параметрах системы и заданной степени отображения внутрисистемных связей.

Особенность имитационного моделирования заключается в 2-х аспектах:

1.При построении математической модели реального стохастического процесса важнейшей частью модели является случайный выбор случайной величины, т. е. сама случайность является основой всего алгоритма. Случайный выбор случайной величины осуществляется с помощью определённых правил.

2.Практическую пользу имитационное моделирование приносит только одновременно с реализацией на компьютере.

Узловой вопрос имитационного моделирования, случайный выбор случайной величины, обычно называют единичным жребием или методом Монте-Карло.

Достоинства имитационного моделирования:

1. Универсальность, т. е. с помощью имитационного моделирования можно описать практически любые вероятностные системы.

2. Возможность описания динамических систем в ускоренном масштабе времени.

3. Экономичность.

Недостатки имитационного моделирования.

1. Очень высокая трудоёмкость моделирования. Для реализации имитационной модели необходимо обработать громадное количество фактического материала, построить эмпирические зависимости и распределения, сравнить их с теоретическими, и т. д.

Следствия (из 1 недостатка):

- имитационное моделирование целесообразно применять только тогда, когда специалист убедился, что ни один другой тип модели в данном случае некорректен.

- имитационное моделирование имеет практическую ценность только при использовании компьютера.

2. Необходимость обширного фактического материала.

3. Реализация имитационной модели позволяет выявить закономерность в случайности, но не даёт оптимального результата, т. е. имитационная модель не содержит в себе целевую функцию.

Имитационное моделирование можно рассматривать как математический эксперимент над вероятностной системой.

Обозначим через

А₁, А₂, ..., А_n события, состоящие в том, что система из исходного состояния в момент τ перейдет в какое-либо i-ое состояние, i = 1 ÷ n

Тогда обозначим вероятности перехода P₁, P₂, …, P_n.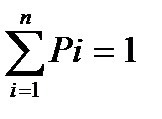

Вопрос состоит в том, как сформулировать единичный жребий таким образом, чтобы выбор любого из i-ых событий происходил бы с i -ой вероятностью этого события.

Рассмотрим луч вещественных чисел в интервале от0 до1

Р₁ Р₂ Р_n 1

Этот интервал заполним числами P_i(вероятности), причём длину каждого кусочка возьмём с величиной конкретной вероятности.

Предположим, что мы каким-то образом можем получить случайную величину ξ (кси), равномерно распределённую в интервале от0 до1.

ξj -определенное значение данной величины.

Будем сравнивать эту величину с величиной 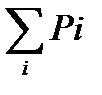Как только окажется, что наша 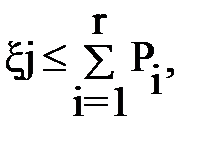то это значит, что мы выбрали r - ое случайное событие.

Пример.

A i
P i	0,11	0,24	0,45	0,05	0,15
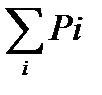
	0,11	0,35	0,80	0,85

ξ j = 0,64

0,64 < 0,11

0,64 < 0,35

0,64 < 0,8 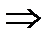мы выбираем 3-е событие.

Когда имитационная модель реализуется на компьютере, то и единичный жребий должен реализоваться в самом компьютере.

Методы получения случайной величины с равномерным распределением на интервале от0 до1 (ξ)

Программы, реализующие на компьютере последовательность случайных чисел ξj, называются генераторами или датчиками случайных чисел.

Идеальный генератор (или датчик) должен формировать последовательность чисел ξj,которые обладали бы следующими свойствами:

1. Последовательность чисел должна быть равномерно распределена на интервале от 0 до 1.

2. Числа должны быть статистически независимыми.

1 Метод: Метод физических датчиков.

Основан на использовании самих физических приборов, имеющихся в компьютере, и на измерении физических параметров этих приборов.

Достоинства: обеспечение высокого быстродействия.

Недостатки: используя данный метод невозможно повторить какую-то определённую реализацию процесса. Поэтому для экономических систем данный метод используется редко.

2 Метод: Метод псевдослучайных чисел (метод Фон Неймана).

Алгоритм: Берётся любая величина, состоящая из 2n цифр, возводится в квадрат; от полученного значения слева и справа отбрасывается по n цифр; оставшаяся величина снова возводится в квадрат и т. д.

Пример: получение равномерно распределённой случайной величины из интервала от0 до1 с плотностью 0,0001

X₁=0.2061 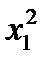=04/2477/21

X₂=0.2477 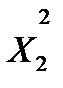=06/1355/29
X₃=0.1355