Закон равномерной плотности.

f (x) f (x) = ,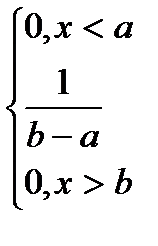

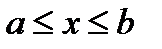
a b х

P (x) =

F(x)

a b x

F(x) =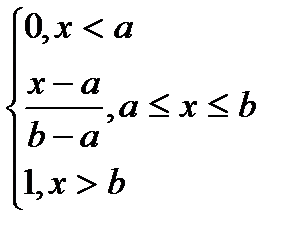

Для случая, когда а=0; в=1:

f (x) F(x)

1 1

x x

0 1 0 1

f(x) = 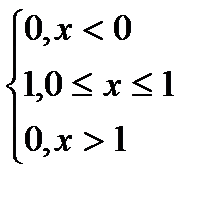F(x) =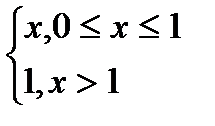

Метод обратных функций при имитации случайного процесса.

Графическое и аналитическое решение.

Данный метод является наиболее употребляемым и основан на следующей теореме:

Теорема: Пусть имеется некоторая случайная величина X, имеющая функцию распределения F(x). Тогда другая случайная величина Y=F(x) равномерно распределена на интервале от 0 до1.

Пусть получена определённая реализация псевдослучайной величины ξj. Приравняем её к функции распределения F(x) (ξj=F(x)) и отсюда найдём значение Xj

F (x)

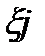
xj x

В случае неизвестной функции распределения иногда пользуются эмпирической функцией плотности распределения, но это не всегда корректно.

f (x) f (x)

ξj

ξj

Xj (x)i 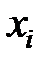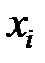xi

Рассмотрим аналитическое решение для закона

равномерной плотности.

F=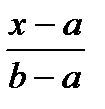

x-a=F(b-a)

x=a+F(b-a) Xj=a+ ξj(b-a)

для показательного закона

F= 1 - e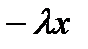

e 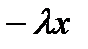= 1 – F

ln(1-F) =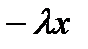

xj = - 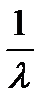ln(1- ξj)

Метод кусочных аппроксимаций при имитации случайного процесса.