Методы решения задач нелинейного программирования

Универсального метода не существует. Различаются 2 группы методов:

· Детерминированные

· Статистические

1) В группе детерминированных методов:

1.1. Градиентный………………………..

1.2. Метод наискорейшего спуска (подъема)

1.3. Графический

2) Статистические методы включают:

2.1. Метод Монте-Карло (метод случайных испытаний)

2.2. Метод направленного случайного поиска

2.3. Метод статистического градиента

Пример использования метода 1.3.

Задача: Найти, спроектировать склад прямоугольной формы по критерию min строительных затрат.

Ограничения:

1. 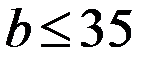м – ширина

2.

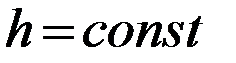
3.

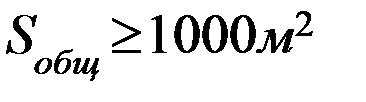
Строительная стоимость 1 м² склада у торцевой стороны 780 руб., а у длинной 200 руб.

b a

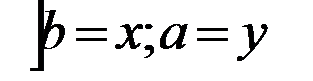
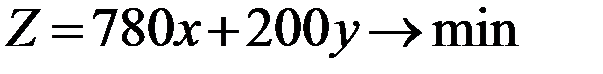
Ограничение: x>0, y>0

X<35

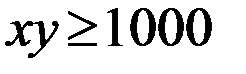
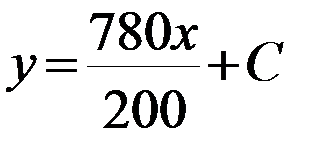
tg - угол наклона целевой функции

y A

x

10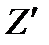

0 Z 10 16 35 X

Z=780*16+200*62,5=224980 руб.

tg угла наклон целевой функции равен первой производной от нелинейного ограничения.

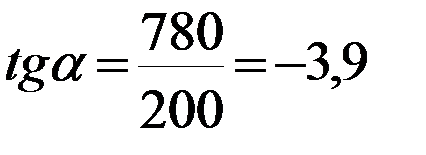
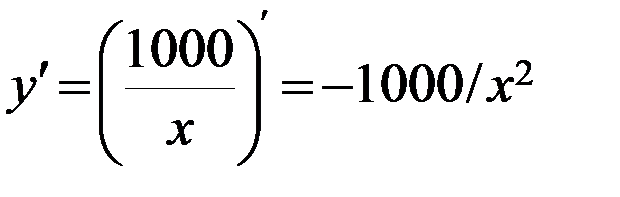
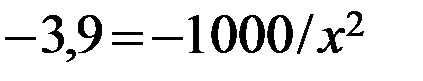
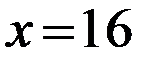
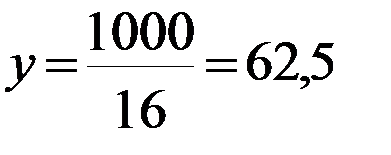
Градиентные методы:

Эти методы применяются для решения задач выпуклого программирования, у которых ограничения линейны, а целевая функция нелинейная и выпукла. Идея проста, а процесс вычислений сложен.

y

B

F

ОДЗ C

A

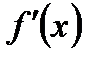D

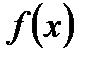
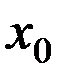E x

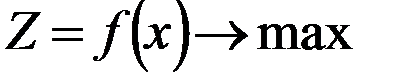
Очевидно, при перемещении функции по направлению градиента ее значение возрастает. Считается, что задан наклон касательной, начальной точки 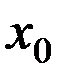, мы двигаемся по градиенту (нормами к касательной) и это самый короткий путь.

На каждом шаге надо проверить, не вышли ли мы за границы области. В каком-то месте условия функции пересекает ОДЗ в точки F.

Из точки F мы двигаемся в точку А, что ухудшает значение целевой функции, или можно двигаться к точки В – это улучшает значения целевой функции. После достижения точки В, надо проверить движение к точке С. Оптимальное решение считается найденным, когда движение в сторону ухудшает значение целевой функции.

«+» Метод точный, несложный по идее, за счет применения ЭВМ трудоемкость значительно снижается.

Метод наискорейшего спуска (подъема)

Включает 5 шагов:

1. выбирается некоторая начальная точка, которая является допустимым решением задачи. В этой точки вычисляется градиент целевой функции.

2. из начальной точки осуществляется движение по градиенту до тех пор, пока целевая функция 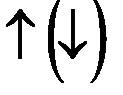при решении .

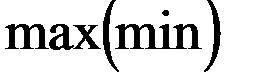3. по достижении границ допустимых решений дальнейшее движение по градиенту прекращается.

4. если граница ОДЗ линейна, то осуществляется движение от одной вершины к другой.

5. если ОДЗ нелинейно и не выпукла, то осуществляется движение вдоль границы. ОДЗ, проверяются локальные и находятся глобально оптимальным.

Наивыгоднейшим из возможных направлений является такое, где max cos 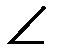между этими направлением и градиентом.