Пример задачи оптимизации и её решение
Симплекс-методом.
Необходимо загрузить судно в порту 3-мя родами груза а, б, в. Грузоподъёмность судна = 2000т (Qp); грузовместимость(W) = 3080м3; удельный погрузочный объём каждого груза: Wа =2, 1м3/т
Wб = 1, 5м3/т
Wв = 1, 7м3/т
Max возможное время погрузки (Тnmax) = 36ч = 2160 мин
Удельное время погрузки каждого рода груза:
tа = 0, 8мин/т
tб = 0, 9мин/т
tв = 1, 3мин/т
Имеется в порту в наличии груза:
а = 900т
б = 1300т
в = неограниченное количество
За перевозку 1т груза взимается провозная плата:
Са = 8 у. е.
Сб = 7, 5 у. е.
Св = 7 у. е.
Необходимо составить оптимальный план загрузки судна на max дохода
Обозначим: х1 – количество груза а, загруженного в оптимальном плане.
х2 – количество груза б, загруженного в оптимальном плане. 
х3 – количество груза в, загруженного в оптимальном плане.
Целевая функция - доход
Z = 8x1 + 7, 5x2 + 7x3 → max
Ограничения. 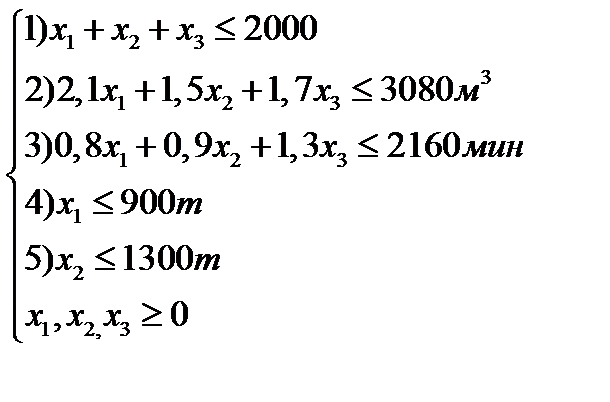
Перейдём от системы неравенств к системе равенств, добавляя свободные переменные.
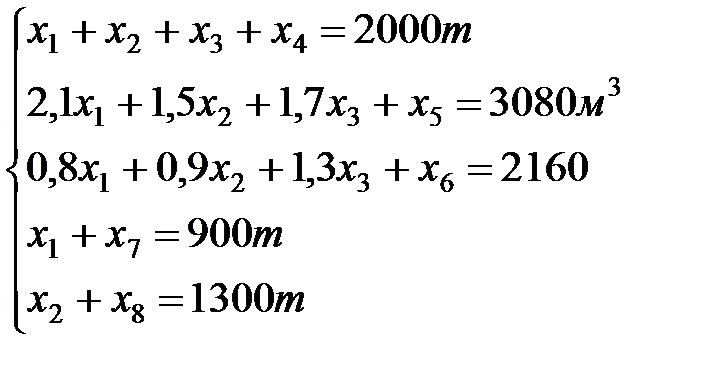
х4– неиспользуемая грузоподъёмность
х5 – неиспользуемая грузовместимость
х6 – неиспользуемое до max время
погрузки.
х7 – недопогруженное количество груза а.
х8 – недопогруженное количество груза б.
Представим условия (т. е. ограничения) в виде векторов.
Р1 =  Р2 =
Р2 =  Р3 =
Р3 = 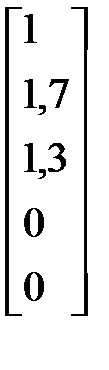 Р4 =
Р4 = 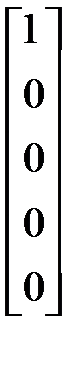
Р5 = 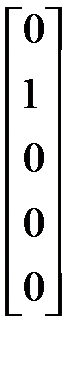 Р6 =
Р6 = 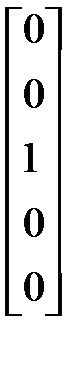 Р7 =
Р7 = 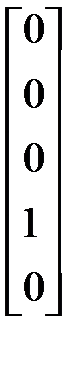 Р8 =
Р8 = 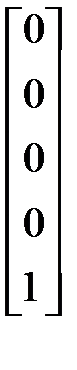 Р0 =
Р0 = 
Вектора Р1, Р2, Р3, образованные из коэффициентов при реальных переменных, называются структурными.
Вектора Р4, Р5, Р6, Р7, Р8 называются линейно не зависимыми (свободными) векторами, Ро – вектор решений.
Данная задача решается относительно m линейно независимых базисных векторов. В данном случае, это свободные векторы (образующиеся из коэффициентов при свободных переменных) Р4 - Р8.
Алгоритм решения предусматривает построение симплекс-таблиц.
| Сi | Сj | 7, 5 | ||||||||
| базис | P0 | P1 | P2 | P3 | P4 | P5 | P6 | P7 | P8 | |
| P4 | ||||||||||
| P5 | 2, 1 | 1, 5 | 1, 7 | |||||||
| P6 | 0, 8 | 0, 9 | 1, 3 | |||||||
| P7 | ||||||||||
| P8 | ||||||||||
| Zj | ||||||||||
| Zj - Cj | - 8 | - 7, 5 | - 7 |
Z j – симплекс-оценка
Zj = 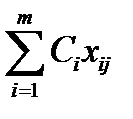
Z j – Cj – признак оптимальности в симплекс-методе.
Если задача решается на max и значение последней строки ≥ 0 по всем столбцам, то план является оптимальным.
Если задача решается на min и значение последней строки 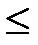 0, то план так же является оптимальным.
0, то план так же является оптимальным.
Если при решении задач на max. хотя бы у одного вектора значение
Zj – Cj < 0, то план не оптимален и требует улучшения.
В общем виде первоначальная симплекс-таблица выглядит следующим образом:
| Ci | Cj | c1 | - | cj | - | C k | - | cn | |
| базис | Р0 | Р1 | - | Рj | - | P k | - | Pn | |
| c1 | P1 | x1 | x11 | x1j | x1 k | x1n | |||
| C2 | P2 | x2 | x21 | x2j | x2 k | x2n | |||
| - | - | - | - | - | - | - | - | - | - |
| Ci | Pi | xi | xi1 | xi j | xi k | xi n | |||
| - | - | - | - | - | - | - | - | - | - |
| Cr | Pr | xr | xr1 | xr j | xr k | xr n | |||
| - | - | - | - | - | - | - | - | - | - |
| Cm | Pm | xm | xm1 | xm j | xm k | xm n | |||
| Zj | z1 | z j | z k | z n | |||||
| Zj - Cj | z1-c1 | z j-C j | z k-C k | z n-C n |
Симплекс-метод . Алгоритм перехода от одного допустимого плана к другому.
Данный алгоритм позволяет превратить неоптимальный план в оптимальный.
Алгоритм имеет следующие этапы:
I. Определятся вектор, который вводится в базис.
Это вектор, который имеет max. нарушение признака оптимальности.
Столбец, который соответствует вводимому в базис вектору, называется ключевым, его индекс обозначается буквой k .
В нашем примере k = 1
II. Определяется вектор, который выводится из базиса. Это тот вектор, у которого имеет место следующее соотношение.
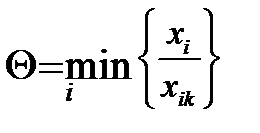 для xik > 0
для xik > 0
xi – элементы вектора решений (столбца Р0)
xik – элементы ключевого столбца.
Строка, которая соответствует минимуму, т. е. выводимому из базиса вектору, называется ключевой строкой, её индекс обозначается буквой r. Элемент таблицы, который находится на пересечении k-ого столбца и r-той строки, называется генеральным элементом и обозначается xrk.
III. Определяется новые значения элементов вектора решений.
Р’0 = P0 - ΘPk
х’i = xi - Θxik
Для ключевой строки значение Р0 = Θ, т.е. х’r = q
IV. Определяется новое значение ключевой строки
x’r j = 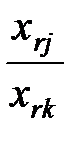
V. Определяются новые значения всех остальных элементов симплекс-таблицы
x’ij = xij - 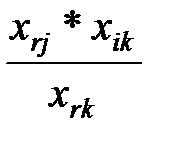
Где 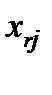 – элемент данного вектора в ключевой строке.
– элемент данного вектора в ключевой строке.
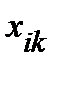 – соответствующий элемент в ключевом столбце.
– соответствующий элемент в ключевом столбце.
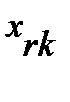 – генеральный элемент.
– генеральный элемент.
| Базис | P0 | 7,5 | ||||||||
| Cj Ci | P1 | P2 | P3 | P4 | P5 | P6 | P7 | P8 | ||
| P4 | -1 | |||||||||
| P5 | 1, 5 | 1, 7 | -2, 1 | |||||||
| P6 | 0, 9 | 1, 3 | -0, 8 | |||||||
| P1 | ||||||||||
| P8 | ||||||||||
| Zj | ||||||||||
| Zj - Cj | -7, 5 | -7 |
Дата добавления: 2019-12-09; просмотров: 889;











