Глава 2. Общая задача линейного программирования

Постановка задачи

В общем виде задача линейного программирования записывается следующим образом:

Дано:

1. Множество переменных (неизвестных) задачи

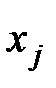для

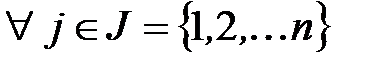
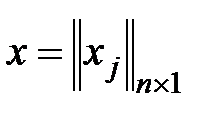- вектор столбец переменных (неизвестных) задачи

2. Множество допустимых решений задачи Q (система условий задачи), задаваемое в виде системы линейных ограничений

a₁₁·x₁ + … + a_1j·x_j +…+ a_1n·x_n = b₁

…………………………………..

a_i1·x₁ + … + a_ij·x_j +… + a_in·x_n = b_i

…………………………………..

Q=

a_k1·x₁ + … + a_kj·x_j+… + a_kn·x_n = b_k

a_{k+1 1}·x₁ + … + a _{k+1 j}·x_j+…+ a _{k+1 n}·x_n≤ b _k+1

…………………………………..

a_m1·x₁ + … + a_mj·x_j+ … + a_mn·x_n≤ b_m

x_j≥0 для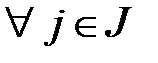

3. Функционал задачи (линейная форма задачи)

F(x)=f₁·x₁ + … + f_j·x_j+… + f_n·x_n

F(x)=f·x,

где

f=(f₁, f₂, … f_j, … , f_n) – вектор строка коэффициентов функционала.

4. Матрица условий задачи

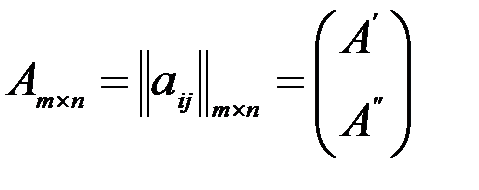
5. Вектор столбец правой части ограничений

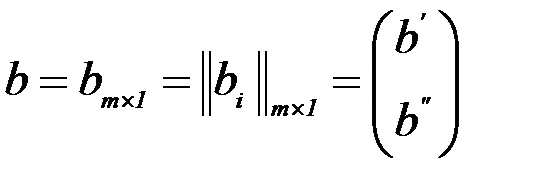
6. Матричная форма задачи оптимизации

Q=

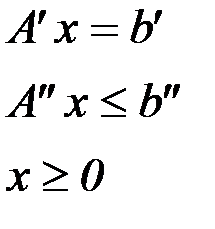
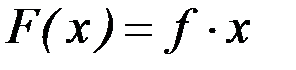
Если ищется максимум функционала

Найти: 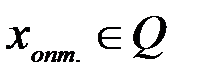такое, что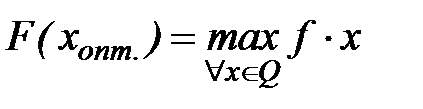

Если ищется минимум функционала

Найти: 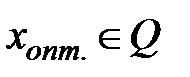такое, что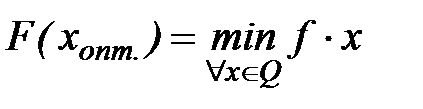

Область Q, заданная системой линейных уравнений и неравенств, представляет собой выпуклый многогранник в n-мерном пространстве, а экстремум линейной функции 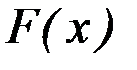достигается в его вершинах.

Канонической формой модели линейного программирования является модель, в которой система ограничений полностью задается системой линейных уравнений

.

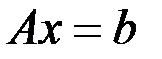Задача линейного программирования, записанная в общем виде, легко сводится к канонической форме путем ввода дополнительных неотрицательных переменных 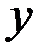, которые с помощью единичной матрицы 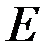превращают систему неравенств 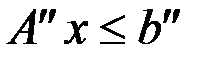в систему уравнений (равенств)

.

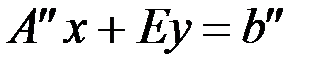В функционал задачи переменные 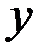войдут с нулевыми коэффициентами.

Во всех случаях, когда задача линейного программирования разрешима, ее решение сводится к упорядоченному перебору вершин n-мерного многогранника.