Геометрическая интерпретация задачи линейного программирования

Пусть имеется система уравнений

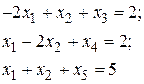(4.6)

и целевая функция

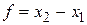. (4.7)

Требуется найти неотрицательные значения переменных, удовлетворяющих условиям (4.6) и минимизирующих функцию (4.7). Поскольку функцию удобнее максимизировать, перейдем к другой функции .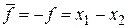

В данном случае число уравнений 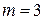, а число переменных 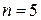. Соответственно имеется 3 базисных переменных и 2 свободных. Это дает возможность проиллюстрировать решение геометрически.

Выберем в качестве базиса переменные 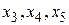и разрешим систему (4.6) относительно этих переменных. Получим

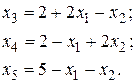(4.8)

По условию задачи переменные могут принимать только неотрицательные значения, т.е. областью допустимых значений переменных будет область, определяемая условиями

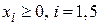. (4.9)

Каждое из неравенств (4.9) определяет полуплоскость на плоскости 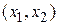. При этом в одной полуплоскости выполняется условие 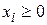, в другой 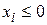. Полуплоскости разделяются прямыми, которым соответствуют условия .

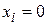Рассмотрим, например, первое уравнение

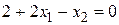, (4.10)

соответствующее условию .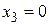

Прямая, соответствующая этому равенству приведена на рис. 4.3. Условие 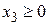определяет ту полуплоскость, в которой содержится начало координат. Это легко подтверждается подстановкой в (4.10) координат .

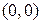Подобные же построения приведены на рис. 4.2 для всех .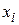

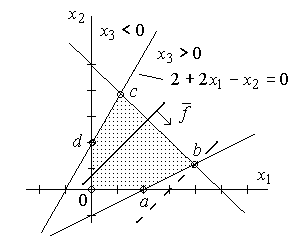
Рис. 4.2. Графическое решение задачи линейного программирования

Допустимой областью является заштрихованный многоугольник 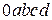. Допустимая область является замкнутой и выпуклой, так как представляет собой пересечение выпуклых областей, определяемых условиями .

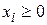Проведенное построение позволяет дать геометрическую трактовку базисному решению. Так как каждая прямая на рис. 4.2 соответствует обращению в нуль одной из переменных, то в точках пересечения двух прямых будут обращаться в нуль две, т.е. 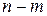переменных. Но 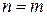есть число свободных переменных, обращение которых в нуль дает одно из базисных решений. Таким образом, точки пересечения прямых 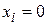определяют базисные решения.

Не все базисные решения являются допустимыми. Ими являются только вершины многоугольника допустимых решений.

Рассмотрим теперь условие обращения в нуль целевой функции. Геометрически, при любом , выражение для целевой функции определяет прямую, проведенную под углом 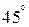к оси абсцисс, причем увеличению соответствует перемещение по стрелке, как это показано на рис. 4.2. Эта прямая будет совместима с допустимым решением задачи только тогда, когда она имеет общие точки с областью допустимых решений. Максимальное значение получится при крайнем положении прямой, которое показано пунктиром. Для выпуклого многоугольника такая прямая обязательно проходит хотя бы через одну из вершин, которые, как мы знаем, соответствуют допустимым базисным решениям. Отсюда следует важный вывод: решение задачи линейного программирования, обращающее в максимум целевую функцию , обязательно лежит среди допустимых базовых решений.

Данный вывод легко обобщается на случай произвольных и 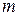, когда 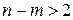. Условия ограничений определят гиперплоскости в 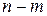-мерном пространстве, а условия 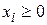– полупространства, ограниченные гиперплоскостями. Допустимое множество будет представлять собой выпуклый многогранник.

Целевая функция линейна, соответственно оптимум всегда глобальный. Функция 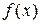не имеет стационарных точек, следовательно, оптимум достигается на границе допустимого множества.

Среди граничных точек допустимого множества существуют крайние точки, являющиеся пересечением отдельных граней, т.е. представляющие собой базисные решения. Оптимум достигается либо в одной крайней точке, либо на множестве крайних точек. Это означает, что решение задачи линейного программирования обязательно лежит среди допустимых базисных решений.

Отсюда ясен путь решения задачи. Поскольку число допустимых базисных решений конечно, то можно найти все такие решения и для каждого из них вычислить . Окончательным решением будет то решение, для которого максимально. Такой путь может быть весьма трудоемким, т.к. число базисных решений может быть велико. Существуют более рациональные способы направленного перебора, одним из которых является симплекс-метод.