Модифицированный симплекс-метод
(µ-метод).
Рассмотрим 2-ой подход к поиску базиса. Это тот случай, когда условия задачи (все или часть из них) выражены строго равенствами. Для решения таких задач применяется М-метод (метод вычисления с искусственным базисом).
Для составления первого допустимого плана в систему ограничений вводят искусственные переменные (векторы), которые имеют не «нулевую» цену, как свободные вектора, а большую (М) цену. Значение М предполагается очень большим.
Образно говоря, искусственные векторы могут рассматриваться, как свободные векторы, за использование которых взимается большой штраф. При этом штраф столь велик, что использование этих векторов в конечном оптимальном решении не допускается.
Пример: Общая постановка задачи М-метода
Дано: m - количество типов судов; i - индекс типа судна;
n - количество линий движения; j - индекс линии;
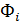 - количество судов каждого типа;
- количество судов каждого типа;
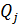 - грузооборот каждой линии за планируемый период;
- грузооборот каждой линии за планируемый период;
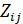 - провозная способность i-го типа судна на j-ой линии за планируемый период;
- провозная способность i-го типа судна на j-ой линии за планируемый период;
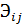 - расходы i-го типа судна на j-ой линии за планируемый период.
- расходы i-го типа судна на j-ой линии за планируемый период.
Необходимо так расставить суда по линиям, чтобы выполнить заданный грузооборот с min общими расходами.
Сформулируем математическую постановку задачи
Искомая переменная - 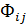 - количество судов i-го типа, закрепленное за j-ой линией в оптимальном плане
- количество судов i-го типа, закрепленное за j-ой линией в оптимальном плане
Ограничения
1) 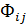 ³ 0 – количество судов i-го типа, закрепленное за j-ой линией, д.б. величиной неотрицательной;
³ 0 – количество судов i-го типа, закрепленное за j-ой линией, д.б. величиной неотрицательной;
2) 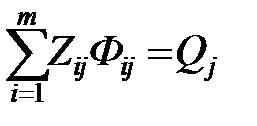 – на каждую линию необходимо расставить такое количество судов, чтобы выполнить запланированный грузооборот;
– на каждую линию необходимо расставить такое количество судов, чтобы выполнить запланированный грузооборот;
3) 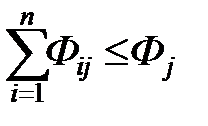 – необходимо использовать флота не более, чем имеется в наличии.
– необходимо использовать флота не более, чем имеется в наличии.
Целевая функция 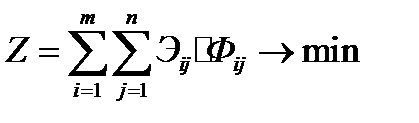
Расстановка грузовых судов по линиям симплексным М-методом (на минимум эксплуатационных расходов).
Пример:
Дано: 1. 2 типа грузовых самоходных судов (m=2) i=1,2
2. 3 грузовые линии движения судов (n=3) j=1,2,3.
3. Количество судов каждого типа: 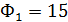 ,
, 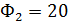
4. Грузооборот на каждой линии, млн. т. км.
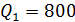
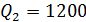
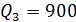
5. Zij – провозная способность судна i-того типа на j-той линии за навигацию, млн. т. км.:
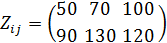
6. Эij – эксплуатационные расходы судна i-того типа на j-той линии за навигацию, тыс. усл. руб.:

Цель задачи: Необходимо так расставить грузовые суда по линиям, чтобы выполнить заданный план перевозок с минимальными эксплуатационными расходами.
Алгоритм решения.
1. Составление ограничений и целевой функции.
Ограничения:
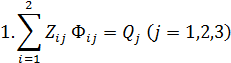
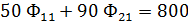
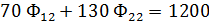
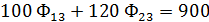
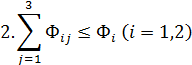
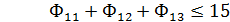
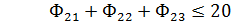
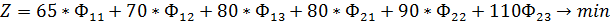
2. Так как при решении задачи М-методом для получения начального базисного плана расстановки судов необходимо иметь единичную диагональную матрицу и систему равенств, преобразуем систему ограничений и функционал цели к виду, обеспечивающему необходимое количество единичных векторов , т.е. в каждое из ограничительных уравнений добавляем по одному вектору.
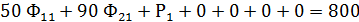
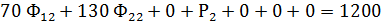
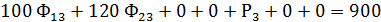
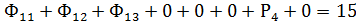
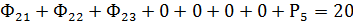
Таким образом получим равенства и единичные векторы Р1, Р2 и Р3 – искусственные векторы, которые показывают недовыполнение плана перевозок на линиях.
Р4 и Р5 – свободные векторы, которые показывают недоиспользованное количество флота.
Искусственные вектора отличаются от свободных тем, что они имеют очень большую цену (М), которую можно рассматривать как штраф за невыполнение плана перевозок . Свободные вектора, показывающие избыток судов, имеют нулевую цену.
После преобразования функционал цели будет иметь вид:
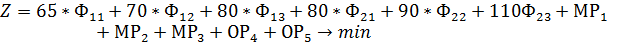
Свободные вектора с нулевой ценой в функционал цели обычно не записываются.
3. После произведенных преобразований составляем симплексную таблицу и заполняем ее исходными данными.
Таблица 1
/ AwBQSwMEFAAGAAgAAAAhAJ5BS5bdAAAACAEAAA8AAABkcnMvZG93bnJldi54bWxMj81OwzAQhO9I fQdrkbhRJ1DREOJUFT8nOKQpB45uvCRR43UUu0ng6dmKAxx3ZjT7TbaZbSdGHHzrSEG8jEAgVc60 VCt4379cJyB80GR05wgVfKGHTb64yHRq3EQ7HMtQCy4hn2oFTQh9KqWvGrTaL12PxN6nG6wOfA61 NIOeuNx28iaK7qTVLfGHRvf42GB1LE9Wwfr5tSz66entu5BrWRSjC8nxQ6mry3n7ACLgHP7CcMZn dMiZ6eBOZLzoFKwSnhIU3Mb3IM5+vGLh8CvIPJP/B+Q/AAAA//8DAFBLAQItABQABgAIAAAAIQC2 gziS/gAAAOEBAAATAAAAAAAAAAAAAAAAAAAAAABbQ29udGVudF9UeXBlc10ueG1sUEsBAi0AFAAG AAgAAAAhADj9If/WAAAAlAEAAAsAAAAAAAAAAAAAAAAALwEAAF9yZWxzLy5yZWxzUEsBAi0AFAAG AAgAAAAhAB/jQFvjAQAA3AMAAA4AAAAAAAAAAAAAAAAALgIAAGRycy9lMm9Eb2MueG1sUEsBAi0A FAAGAAgAAAAhAJ5BS5bdAAAACAEAAA8AAAAAAAAAAAAAAAAAPQQAAGRycy9kb3ducmV2LnhtbFBL BQYAAAAABAAEAPMAAABHBQAAAAA= " strokecolor="black [3040]"/> 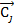 Ci
Базис
Ci
Базис
| М | М | М | ||||||||||
| Po | Ф11 | Ф12 | Ф13 | Ф21 | Ф22 | Ф23 | P1 | P2 | P3 | P4 | P5 | ||
| М P1 | 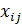
| 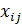
| 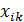
| ||||||||||
| М P2 | 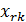
| ||||||||||||
| М | P3 | ||||||||||||
| О | P4 | ||||||||||||
| О | P5 | 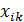
| |||||||||||
| Zj | 50М | 70М | 100М | 90М | 130М | 120М | М | М | М | О | О | ||
| Zj – Cj | 50М -65 | 70М-70 | 100М-80 | 90М-80 | 130М-90 | 120М-110 | М-М=0 |
В таблице Ро – вектор решений, который составляется из правых частей уравнений и численно выражает грузооборот и количество судов.
Ci – цена базисных векторов;
Cj – цена структурных, искусственных и свободных векторов.
4. Определяем Zj и разности Zj - Cj для каждого вектора.
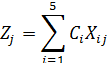
где Хij – элементы i-той строки и j-го столбца-вектора .
Разность Zj - Cj показывает оптимальность плана, т.е. является условием оптимальности.
Если решаем задачу на min критерия, то решение будет оптимальным при условии
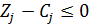
Если же решаем задачу на max критерия, то для оптимальности должно выполняться условие
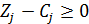
Далее реализуем алгоритм симплекс-метода:
1. Выбираем вектор, который будем вводить в базис. Он будет соответствовать наибольшему нарушению, т.е. наибольшей разности
Zj - Cj .
Наибольшая разность равна 130М-90, что соответствует вектору Ф22 . Обозначим этот вектор Рк.
2. Определяем в базисе вектор, который будем выводить из базиса, т.е. будем замещать вектором Рк. Для этого производится деление элементов Хi из столбца Ро на соответствующие положительные элементы Хiк вектора Рк. В таблице замещается вектор, для которого достигается минимум отношения.
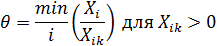
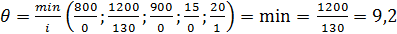
Следовательно, будем выводить из базиса вектор Р2, обозначим его как Рr. Элемент на пересечении векторов Рк (ключевой столбец) и Рr (ключевая строка) называется генеральным элементом. Обозначаем его Хrк, в нашем случае Хrk = 130.
Вектор Рк (Ф22) вводим в базис, а вектор Рr (Р2) выводим. Для этого строим новую симплексную таблицу 2.
Таблица 2
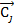 Ci
Базис
Ci
Базис
| М | М | М | ||||||||||
| Po | Ф11 | Ф12 | Ф13 | Ф21 | Ф22 | Ф23 | P1 | P2 | P3 | P4 | P5 | ||
| М P1 | |||||||||||||
| 90 Ф22 | 9,2 | 0,54 | 0,1 | ||||||||||
| М | P3 | ||||||||||||
| P4 | |||||||||||||
| P5 | 10,8 | -0,54 | -0,01 | ||||||||||
| Zj | 50М | 100М | 90М | 120М | М | М | О | О | |||||
| Zj – Cj | 50М -65 | 48-70 | 100М-80 | 90М-80 | 120М-110 | 9-М |
3. Затем определяются новые значения элементов вектора решений по формуле:
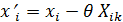
Для вновь введенного в базисе вектора (Ф22) 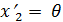
Находим для остальных:
Х1= 800-9,2*0 = 800
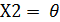 = 9,2
= 9,2
Х3= 900-9,2*0 = 900
Х4= 15-9,2*0 = 15
Х5= 20-9,2*1 = 10,8
4. В таблице 2 заполняется строка вводимого в базис вектора Ф22 (ключевая строка). Для этого все элементы строки Р2 в таблице 1 делятся на генеральный элемент (130) и заносятся в соответствующие клетки таблицы 2. В этой строке базиса ставится цена вектора Ф22, т.е. 90.
5. Все остальные элементы новой таблицы 2 определяются по формуле:
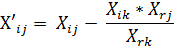
Из формулы видно, что :
1) В новой матрице, в столбце, соответствующем ключевому столбцу таблицы 1 все элементы будут равны нулю и лишь на месте генерального элемента будет 1.
2) Если в ключевом столбце (вектор Рк) какой-либо элемент Хik=0, то все элементы этой строки (где находится Хik=0) переписываются в новую матрицу без изменения.
В нашем случае без изменения перепишутся строки Р1,Р3,Р4.
3) Если в ключевой строке (вектор Рr) какой-либо элемент Хrj=0, то все элементы j-го столбца переписываются в матрицу 2 без изменения. (столбцы Р11, Р13, Р21, Р23, Р1, Р3, Р4, Р5)
Оставшиеся элементы таблицы 2 определим по приведенной формуле 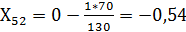
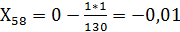
Определяем значения Zj и Zj-Cj в таблице 2, т.е. ищем максимальное нарушение. В нашем случае max нарушение в таблице 2 равно 120 М-110, что соответствует вектору Ф23.
Выше приведенные действия повторяются до тех пор, пока не будут устранены все нарушения оптимальности плана, т.е. во всех случаях Zj-Cj будет ≤ 0.
Расшифровка после решения.
| Сi | Базис | Ро |
| Ф13 | ||
| Ф21 | 8,8889 | |
| Ф22 | 9,2308 | |
| Р4 | ||
| Р5 | 1,883 |
То есть Ф13 = 9
Ф21 = 8,8889
Ф22 = 9,2308
Р4 = 6
Р5 = 1,883
Остальные переменные = 0.
Z = 80*9+80*8,8889+90*9,2308 = 2261,88 тыс. усл. руб.
Проверка ограничений:
1. 90*8,8889 = 800 млн. т.км
2. 130*9,2308 = 1200 млн. т.км
3. 100*9 = 900 млн. т.км
4. 9 < 15 (9+6=15) судов
5. 8,8889+9,2308 < 20 судов
(8,8889+9,2308+1,883 = 20)
Проиллюстрируем применение µ - метода для максимизации дохода по портфелю из 3-х активов, при ограничении max уровня риска всего портфеля. Рассмотрим задачу построения портфеля с целевой функцией достижения max дохода при том ограничении, что max риск портфеля не должен быть выше 1,1.
Допустим, что для выбора есть 3 актива. Их ожидаемая доходность составляет:
А – 0,11
В – 0,15
С – 0,08
Причём риск каждого актива составляет:
А – 1,0
В – 1,2
С – 0,9
Обозначим долю каждого актива из портфеля Wа, Wв, Wc. Значение этих долей определяется портфельным менеджером и является переменной, которая может изменяться для достижения поставленной цели.
Цель: найти такую комбинацию долей каждого актива, которая максимизировала бы целевую функцию при выполнении ограничений.
Математическая постановка данной задачи оптимизации состоит в определении целевой функции и ограничений.
Z = 0,11Wa + 0,15Wв + 0,08Wc → max
Ограничения: 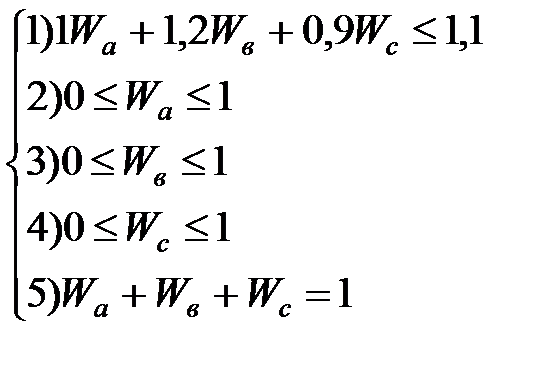
Обозначим: Wa = x1; Wв = x2; Wc = x3,
тогда Z = 0,11x1 + 0,15x2 + 0,08x3 → max
Ограничения:
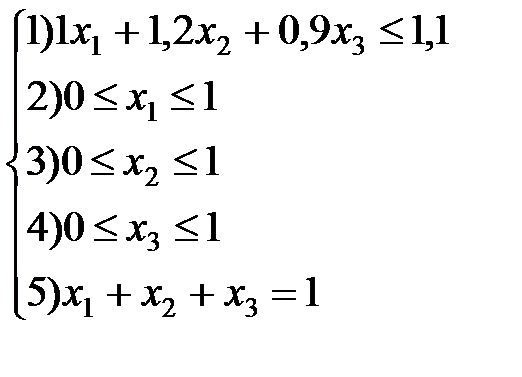
Поскольку в ограничениях имеется равенство используем 2-ой подход к поиску к поиску базиса, т. е. впервые 4 ограничения будут вводится свободные переменные, имеющие нулевую цену в целевой функции и превращающие неравенства в равенства; а в 5-ое ограничение будет вводится искусственная переменная, имеющая большую µ-цену в целевой функции.
Преобразуем ограничения и целевую функцию для нахождения первоначального плана.
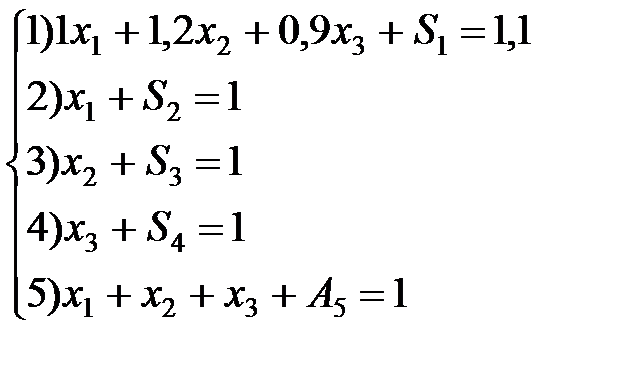
Z = 0,11x1 + 0,15x2 + 0,08x3 - µA5 → max
S1, S2, S3, S4 – свободные переменные, их цена в целевой функции = 0.
Переменная А5 – искусственная переменная, её цена в целевой функции = µ. В данном случае при решении задачи на max значение µ будет большим отрицательным числом. В оптимальном плане значение А5 должно быть = 0.
Построим первоначальную симплекс-таблицу с первым базисным решением.
| Сj | Базис | Р0 | 0,11 | 0,15 | 0,08 | -µ | ||||
| Сi | x1 | x2 | x3 | S1 | S2 | S3 | S4 | A5 | ||
| S1 | 1,1 | 1,2 | 0,9 | |||||||
| S2 | ||||||||||
| S3 | ||||||||||
| S4 | ||||||||||
| -µ | A5 | |||||||||
| -µ | -µ | -µ | -µ | |||||||
| Zj - Cj | -µ-0,11 | -µ-0,15 | -µ-0,08 |
Воспользуемся алгоритмом симплекс-метода, который позволяет превратить не оптимальный план в оптимальный.
I. Определяется вектор, который вводится в базис. Это вектор, имеющий max нарушение признака оптимальности – х2.
II. Определяется вектор, который выводится из базиса
Θ = min 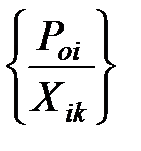 =
= 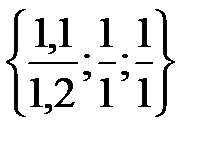 = 0,917 Это вектор S1
= 0,917 Это вектор S1
Для хik > 0
III. Определяется новое значение вектора решений.
P0 = P0 – Θ xik P’2 = 1 – 0,917*0 = 1; P’4 = 1 – 0,917*0 = 1
Р¢1 = q = 0,917 P’3 = 1 – 0,917*1 = 0,083; P'5 = 11 – 0,9177*1 = 0,08
| Сj Сi | базис | P0 | 0,11 | 0,15 | 0,08 | -µ | ||||
| Х1 Wa | X2 Wв | X3 Wc | S1 | S2 | S3 | S4 | A5 | |||
| 0,15 | x2 | 0,917 | 0,833 | 0,75 | 0,833 | |||||
| S2 | ||||||||||
| S3 | 0,083 | -0,833 | -0,75 | -0,833 | ||||||
| S4 | ||||||||||
| -µ | A5 | 0,083 | 0,167 | 0,25 | -0,833 | |||||
| Zj | 0,125-0,167м | 0,125 | 0,112-0,25м | 0,15 + 0,833м | -µ | |||||
| Zj - Cj | 0,015-0,167м | 0,032-0,25м | 0,15 + 0,833м |
Используем правила, упрощающие заполнение симплекс-таблицы
IV. Определяется новое значение ключевой строки.
Х’rj = 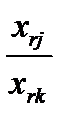
X11 = 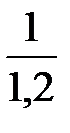 = 0,833
= 0,833
X13 = 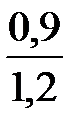 = 0,75 X14 =
= 0,75 X14 = 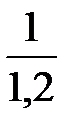 = 0,833
= 0,833
V. Определяются новые значения всех остальных элементов.
X31 = 0 - 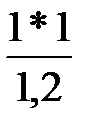 = -0,833
= -0,833
X51 = 1- 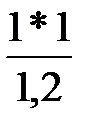 = 0,167
= 0,167
X33 = 0 - 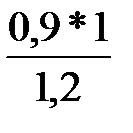 = -0,75
= -0,75
Поскольку в последней строке имеются нарушения, то план не является оптимальным.
Построив ещё несколько таблиц, получим оптимальное решение:
| Сj Ci | базис | Р0 | 0,11 | 0,15 | 0,08 | -µ | ||||
| х1 | х2 | х3 | S1 | S2 | S3 | S4 | A5 | |||
| 0,15 | x2 | 0,5 | -0,5 | -5 | ||||||
| S2 | 0,5 | -1,5 | -6 | |||||||
| S3 | 0,5 | 0,5 | -5 | |||||||
| S4 | ||||||||||
| 0,11 | х1 | 0,5 | 1,5 | -5 | ||||||
| Zj | 0,11 | 0,15 | 0,09 | 0,2 | -0,09 | |||||
| Zj - Cj | 0,01 | 0,2 | -0,09+ µ |
Х1 = 0,15 Х2 = 0,5
Z = 0, 11*0, 5 + 0, 15*0, 5 + 0, 08*0 - µ*0 = 0, 13 – max
Выполнение ограничений:
1*0, 5 + 1, 2*0, 5 + 0, 9*0 = 1, 1
0, 5 < 1 (0, 5 + 0, 5 = 1)
0, 5 < 1 (0, 5 + 0, 5 = 1)
0 < 1 (0 + 1 = 1)
0, 5 + 0, 5 + 0 = 1
Дата добавления: 2019-12-09; просмотров: 809;











