ВЗАИМНО ДВОЙСТВЕННЫЕ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Рассмотрим формально две задачи i и ii линейного программирования, представленные в табл. 2, абстрагируясь от содержательной интерпретации параметров, входящих в их экономико-математические модели.
Таблица 2
| задача i (исходная) | задача ii (двойственная) |
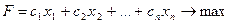 (10)
при ограничениях (10)
при ограничениях
 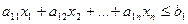 , ,
 , (11)
……………………………, , (11)
……………………………,
 .
и условии неотрицательности
х1³0, х2³0,…, хn³0 (12)
составить такой план выпуска продукции .
и условии неотрицательности
х1³0, х2³0,…, хn³0 (12)
составить такой план выпуска продукции 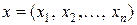 , при котором прибыль от реализации продукции будет максимальной при условии, что потребление ресурсов по каждому виду продукции не превзойдет имеющихся запасов. , при котором прибыль от реализации продукции будет максимальной при условии, что потребление ресурсов по каждому виду продукции не превзойдет имеющихся запасов.
|  (13)
при ограничениях (13)
при ограничениях
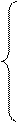 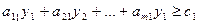 , ,
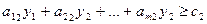 , (14)
……………………………., , (14)
…………………………….,
 .
и условии неотрицательности
y1³0, y2³0,…, yn³0 (15)
составить такой набор цен ресурсов .
и условии неотрицательности
y1³0, y2³0,…, yn³0 (15)
составить такой набор цен ресурсов 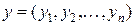 , при котором общие затраты на ресурсы будут минимальными при условии, что затраты на ресурсы при производстве каждого вида продукции будет не менее прибыли от реализации этой продукции. , при котором общие затраты на ресурсы будут минимальными при условии, что затраты на ресурсы при производстве каждого вида продукции будет не менее прибыли от реализации этой продукции.
|
Обе задачи обладают следующими свойствами:
1. В одной задаче ищут максимум линейной функции, в другой — минимум.
2. Коэффициенты при переменных в линейной функции одной задачи являются свободными членами системы ограничений в другой.
3. Каждая из задач задана в стандартной форме, причем в задаче максимизации все неравенства вида «≤» а в задаче минимизации — все неравенства вида «≥».
4. Матрицы коэффициентов при переменных в системах ограничений обеих задач являются транспонированными друг к другу:
для задачи i а 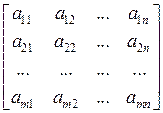
для задачи ii а¢ 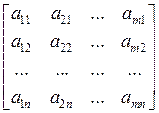
5. Число неравенств в системе ограничений одной задачи совпадает с числом переменных в другой задаче.
6. Условия неотрицательности переменных имеются в обеих задачах.
Две задачи i и ii линейного программирования, обладающие указанными свойствами, называются симметричными взаимно двойственными задачами. В дальнейшем для простоты будем называть их просто двойственными задачами.
Исходя из определения, можно предложить следующий алгоритм составления двойственной задачи.
1. Привести все неравенства системы ограничений исходной задачи к одному смыслу: если в исходной задаче ищут максимум линейной функции, то все неравенства системы ограничений привести к виду «≤», а если минимум - к виду «≥». для этого неравенства, в которых данное требование не выполняется, умножить на (-1).
2. Составить расширенную матрицу системы а1, в которую включить матрицу коэффициентов при переменных а, столбец свободных членов системы ограничений и строку коэффициентов при переменных в линейной функции.
3. Найти матрицу а1′ , транспонированную к матрице а1.
4. Сформулировать двойственную задачу на основании полученной матрицы а1′ и условия неотрицательности переменных.
Дата добавления: 2021-07-22; просмотров: 694;











