Линейного программирования – метод индексов.
Данный метод часто используется при решении задач оперативного планирования. При этом достигается достаточно близкое к оптимальному решение. Возникновение таких методов вызвано тем, что частые изменения в оперативных планах сделали не практичным использование трудоёмких точных методов.
Индексный метод является самым простым приближённым методом решения задач линейного программирования. С его помощью задачи решаются быстро, с min затратами труда и времени. Метод основан на сопоставлении степени целесообразности использования технических средств на том или ином участке работы. Сопоставление производителя с помощью специальных индексов.
Недостаток: при решении задач сопоставляются показатели однотипных технических средств на различных участках работы. При этом сопоставление различных технических средств на каждом из участков работы не производится, т. е. сопоставление показателей матрицы производится для каждой строки по столбцам и не производится для каждого столбца по строкам,  индексный метод обеспечивает результаты решения менее точные, чем метод простейших аппроксимаций. Поэтому, при составлении матрицы, желательно составить такую последовательность строк сверху вниз, чтобы верхняя строка обладала лучшими показателями, а последняя – худшими.
индексный метод обеспечивает результаты решения менее точные, чем метод простейших аппроксимаций. Поэтому, при составлении матрицы, желательно составить такую последовательность строк сверху вниз, чтобы верхняя строка обладала лучшими показателями, а последняя – худшими.
Пример:
Расстановка флота по линиям движения.
m – количество типов грузовых судов; i = 1 ÷ m
n – количество линий движения; j = 1 ÷ n
Фi - количество судов каждого типа.
Gj – грузооборот на каждой линии (млн. т.км за навигацию)
Pij – провозная способность судна i – ого типа при работе на j – ой линии
(млн. тонн/км за навигацию)
Цель: необходимо так расставить имеющийся флот по линиям, чтобы выполнить заданный грузооборот min – ым количеством судов.
Математическая постановка задачи:
Искомая переменная:
Фij - количество судов i-ого типа работающих на j-ой линии
Целевая функция:
Z = 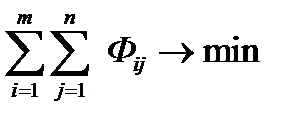
Ограничения:
1. Фij  0
0
2. 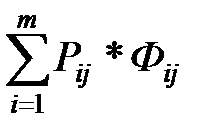 = G
= G 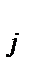
3. 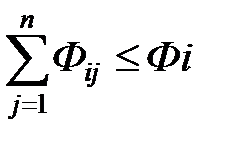
m = 3 n = 5
Ф1 = 6 G1 = 105
Ф2 = 8 G2 = 230 Pij = 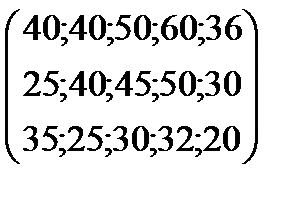
Ф3 = 12 G3 = 270
G5 = 240
G6 = 100
Z = Ф11 + Ф12 + Ф13 + Ф14 + Ф15 +
+ Ф21 + Ф22 + Ф23 + Ф24 + Ф25 +
+ Ф31 + Ф32 + Ф33 + Ф34 + Ф35 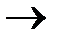 min
min
Ограничения:
1) Фij  0 для
0 для  , i, j.
, i, j.
2) P11Ф11 + Ф21Р21 + Р31Ф31 = 105 = 40Ф11 + 25Ф21 + 35Ф31 = 105
40*Ф12 + 40*Ф22 + 25*Ф32 = 230
= 270
= 240
= 100
3) Ф11 + Ф12 + Ф13 + Ф14 + Ф15 ≤ 6
Ф21 + Ф22 + Ф23 + Ф24 + Ф25 ≤ 8
Ф31 + Ф32 + Ф33 + Ф34 + Ф35 ≤ 12
| j | |||||||
| i | Gj Фi | ||||||
| Х 0,33 | Х 0,33 | Х 0,17 | 1) 0 | 6) 0,4 | |||
| Х 0,5 | 4) 0,2 | 3) 0,1 | Х | Х 0,4 | |||
| 2) 0 | 5) 0,29 | Х 0,14 | Х 0,09 | 1,45 7) 0,43 | |||
Для получения решения строим матрицу.
1. Разместим строки в порядке ухудшения показателей (здесь-провозная способность) – сверху вниз
2. Определяем значения индексов:
U 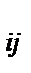 =
= 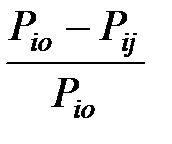 U
U 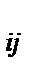 - индекс клетки с адресом ij.
- индекс клетки с адресом ij.
P 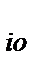 - провозная способность судна i – ого типа при работе на
- провозная способность судна i – ого типа при работе на
базисной линии. За базисную линию принимается
та, на которой достигаются лучшие показатели(max провозной способности). При этом каждый тип судна может иметь свою базисную линию. Если задача решается по показателю наилучшее значение которого – min-ое (например, по показателю себестоимости), то индекс определяется следующим образом:
U 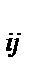 =
= 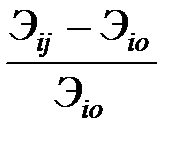
Индекс в данном случае – это число, показывающее относительные потери провозной способности судов при использовании их на других линиях, кроме базисных. Индекс можно рассматривать как штраф, накладываемый за использование судов на других линиях по сравнению с базисной. Чем ближе значение индекса к 0, тем эффективнее использование судов на данной линии. По этому признаку и осуществляется распределение судов по линиям. Распределение начинается с судов, имеющих лучшие показатели (от верхней строки к нижней). На базисной линии закрепляется max возможное количество судов. Если распределены все суда данного типа, то вычёркивается строка. Далее суда ставятся на ту линию, где имеется min значение индекса из всех индексов матрицы, оставшихся после вычёркивания. Шаги решения повторяются, пока не будет выполнен весь грузооборот на всех линиях, или не будут расставлены все имеющиеся суда.
U11 = 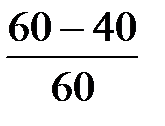 = 0,33 = U12
= 0,33 = U12
U13 = 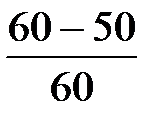 = 0,17
= 0,17
U15 = 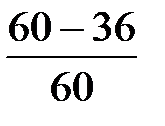 = 0,4
= 0,4
После расстановки судов по линиям, определяем, сколько потребовалось судов, для выполнения грузооборота.
Z = 6 + 8 + 10,45 = 24,45
В резерве осталось 1,55 судна 3-его типа.
Проверка ограничений:
1) 3*35 = 105
2) 2*40 + 6*25 = 230
3) 6*45 = 270
4) 4*60 = 240
5) 2*36 + 1,45*20 = 100
4 + 2 = 6
2 + 6 = 8
3 + 6 + 1,45 < 12
Для получения строго оптимального решения необходимо полученное решение закончить одним из точных методов.
Дата добавления: 2019-12-09; просмотров: 1012;











