Математическая модель и экономическая постановка.

Условия оптимальности плана.

Иногда эту задачу называют – обобщённая транспортная задача. На речном транспорте обобщённая транспортная задача применяется для оптимизации расстановки транспортных и перегрузочных средств по участкам работ.

Обобщённой задача называется потому, что при её решении используются условия оптимальности в общем виде.

Алгоритм решения обобщённой транспортной задачи рассмотрим на примере распределения судов по линиям движения.

m – количество типов судов.

i = 1 ÷ n – индекс конкретного типа судна.

n - количество линий движения.

j = 1 ÷ n – индекс конкретной линии.

Ф 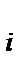- количество судов i – ого типа

П 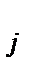- пассажирооборот на каждой линии навигации. (млн. пассаж.км)

Z 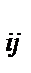- провозная способность судна i – типа при работе на j – ой линии за навигацию (млн. пассаж.км).

Э 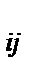- эксплуатационные расходы по судну i – ого типа при работе на j – ой линии за навигацию (у.д.е.).

Необходимо составить такой план расстановки судов по линиям, при котором минимизировались бы эксплуатационные расходы.

Искомая переменная Ф 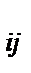- количество флота i – типа, закреплённого на j – ой линией.

Z =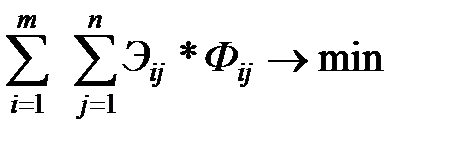

1) Ф 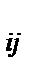≥ 0

2)

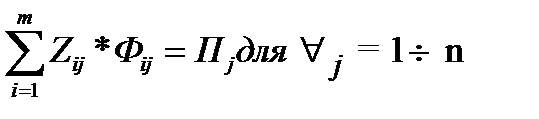
3)

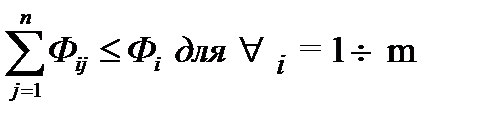
Условия оптимальности для обобщённой транспортной задачи следующие:

План расстановки судов по линиям будет оптимальным ,если выполняются следующие требования:

1) 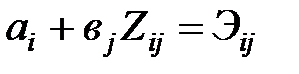для Ф 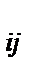> 0 (для заполненных клеток)

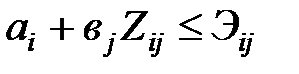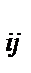2) для Ф = 0

a_i и в_j – потенциалы (оценочные числа);

С помощью 1 – ого уравнения определяются все значения потенциалов а_i и в_j, принимая первый потенциал произвольно.

С помощью 2-го неравенства проверяется оптимальность плана.

Пример:

m = 2 Ф₁ = 5

n = 3 Ф₂ = 7

П₁ = 9 Э₁₁ = 22 Э₁₂ = 14 Э₁₃ = 26

П₂ = 3 Э₂₁ = 16 Э₂₂ = 12 Э₂₃ = 20

П₃ = 6

Z₁₂ = Z₂₂ = 1

Z₁₁ = Z₂₁ = 1,5

Z₁₃ = Z₂₃ = 2