Пример расчёта по алгоритму.
1. Выделяем вектор с max нарушением признака оптимальности, это вектор Р1.
2. Θ = 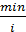
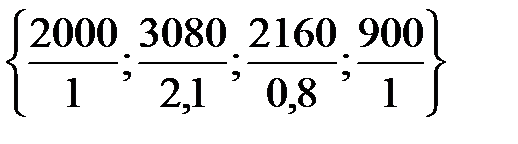 = 900
= 900
Следовательно, ключевая строка будет для вектора Р7 и его мы будем выводить из базиса.
3. х’1 = 2000 – 900*1 = 1100
х’2 = 3080 – 900*2, 1 = 1190
x’3 = 2160 – 900*0, 8 = 1440
x’4 = Θ = 900
x’5 = 1300 – 900*0 = 1300
Правила упрощающие заполнение
симплекс-таблицы.
1) В новой симплекс-таблице значения элементов ключевого столбца будут = 0, а на месте генерального элемента будет стоять 1.
2) Каждая строка, в ключевом столбце которой стоит 0, переписывается без изменений (у нас – Р8)
3) Каждый столбец, в ключевой строке которого стоит 0, также переписывается без изменений (у нас все, кроме Р7).
4. x’rj = 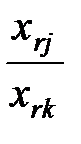 ;
; 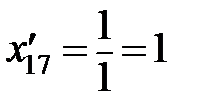
5. x’ij=xij - 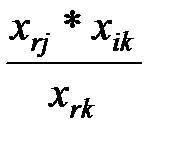
x’47 = 0 - 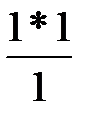 = -1
= -1
x’57 = 0 - 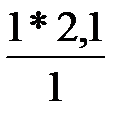 = -2, 1
= -2, 1
x’67 = 0 - 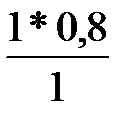 = -0, 8
= -0, 8
Zj = 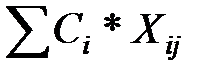 .
.
Поскольку в последней строке имеются нарушения, план не оптимальный.
Рассчитаем целевую функцию для этого плана:
Z = 8*900 = 7200 у. е.
Составим следующую симплекс-таблицу
| Cj Ci | Базис | P0 | 7,5 | |||||||
| P1 | P2 | P3 | P4 | P5 | P6 | P7 | P8 | |||
| P4 | -0, 13 | -0, 67 | 0, 4 | |||||||
| 7, 5 | P2 | 1, 13 | 0, 67 | -1, 4 | ||||||
| P6 | 0, 28 | -0, 6 | 0, 46 | |||||||
| P1 | ||||||||||
| P8 | -1, 13 | -0, 67 | 1, 4 | |||||||
| Zj | 7, 5 | 8, 5 | -2, 5 | |||||||
| Zj - Cj | 1, 5 | -2, 5 |
1. Ключевой столбец (max нарушение) - Р2
2. Θ = 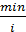
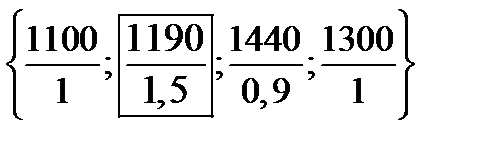 = 794
= 794
Выводим Р5, вводим на его место в базис Р2
3. x’1 = 1100 – 794*1 = 306
x’2 = 794
x’3 = 1440 – 794*0, 9 = 726
x’4 = 900 – 794*0 = 900
x’5 = 1300 – 794*1 = 506
Далее используем правила, упрощающие заполнение симплекс-таблицы
4.
5. x’43 = 1 - 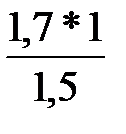 = - 0, 13 x’63 = 0, 28
= - 0, 13 x’63 = 0, 28
x’45 = 0 - 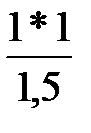 = - 0, 67 x’65 = - 0, 6
= - 0, 67 x’65 = - 0, 6
x’47 = 0, 4 x’67 = 0, 46
Поскольку есть отрицательное значение в последней строке, план не оптимальный.
Z = 7, 5*794 + 3*900 = 13155 у. е.
В итоге после построения ещё нескольких симплекс-таблиц мы, наконец, получили оптимальный план.
| C j i | Базис | Р0 | Р1 | 7,5 Р2 | Р3 | Р4 | Р5 | Р6 | Р7 | Р8 |
| Р4 | -0,24 | -0,59 | -0,12 | |||||||
| 7,5 | Р2 | |||||||||
| Р6 | -0,81 | -0,76 | 0,25 | |||||||
| Р3 | 1,24 | 0,59 | -0,88 | |||||||
| Р7 | ||||||||||
| Zj | 8,67 | 7,5 | 4,12 | 1,32 | ||||||
| Zj - Cj | 0,65 | 4,12 | 1,32 |
Z = 1300*7,5 + 665*7 = 14406 у. е.
Расшифровка решения
х1=0
х2=1300
х3=665
х4=35
х5=0
х6=125
х7=900
х8=0
Проверяем ограничения для полученного оптимального плана:
1) х1 + х2 + х3 = 0 + 1300 + 665 = 1965 < 2000т
х4 = 35 – не используемая грузоподъёмность
2) 1,5*1300 + 1,7*665 = 3080 м3
3) 0,9*1300 + 1,3*665 < 2160 мин
х6 = 125 – сэкономленное время до max
4) 0 < 900
5) х2 = 1300 = 1300
В оптимальном плане в судно грузится 1300т груза «б» и 665т груза «в». При этом, значение целевой функции составит 14 406 у. е.
Дата добавления: 2019-12-09; просмотров: 741;











