Транспортная задача линейного программирования.
Рассмотрим экономико-математическую модель прикрепления пунктов отправления к пунктам назначения.
Имеется m пунктов отправления:
i = 1 ÷ m
Для каждого пункта известны объёмы отправления:Q1, Q2…Qm.
Имеется n пунктов назначения;
j=1 ÷ n
Известна потребность грузов в каждом пункте: V1, V2…Vn.
Задана матрица стоимостей доставки (или расстояний) по каждому варианту Ci j (Li j )
Необходимо рассчитать оптимальный план перевозок, т. е. определить, сколько груза должно быть отправлено из каждого i – ого пункта отправления (от поставщика) в каждый j – пункт назначения(до потребителя) Xi j c min транспортными издержками (или при min общем грузообороте)
Математическая постановка транспортной задачи
Искомая переменная - 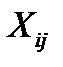
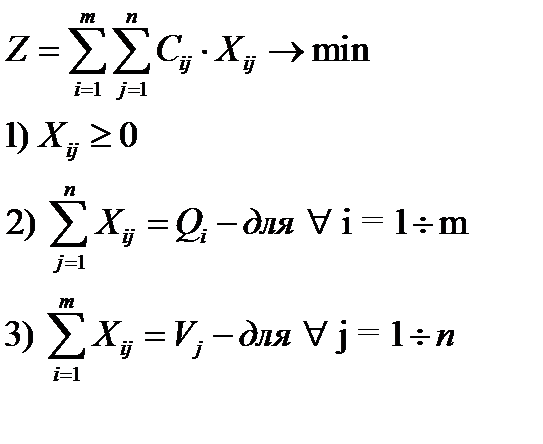
В общем виде данные представляются в таблице
| Потребители (пункты назнач) Пост.(n отпр.) | В1 | В2 | … | Вn | Запасы Qi |
| A1 | X11 C11 | X12 C12 | X1n C1n | Q1 | |
| A2 | X21 C21 | X22 C22 | X2n C2n | Q2 | |
| … | |||||
| Am | Xm1 Cm1 | Xm2 Cm2 | Xmn Cmn | Qm | |
| Потребности Vj | V1 | V2 | Vn |
Для того, чтобы транспортная задача решалась она должна быть закрытой, т. е. должно выполнятся условие:
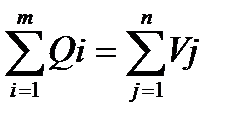
Если задача не закрыта, то её необходимо привести к закрытой форме. В случае, если потребности по пунктам назначения превышают запасы пунктов отправления, вводится фиктивный поставщик с недостающим объёмом отправления.
В случае, если запасы поставщиков превышают запасы потребителей, вводится фиктивный потребитель с необходимым объёмом потребления.
Транспортной задаче присущи следующие особенности:
-распределению подлежат однородные ресурсы;
- условия задачи описываются только равенствами;
- все переменные выражаются в одинаковых единицах измерения;
- во всех равенствах коэффициенты при переменных =1;
-каждая неизвестная встречается только в 2-х равенствах системы ограничений.
Алгоритм метода потенциалов.
Решение задачи методом потенциалов включает следующие этапы:
1. Разработка начального плана;
2. Расчёт потенциалов;
3. Проверка плана на оптимальность;
4. Поиск max звена не оптимальности (если условие оптимальности было нарушено);
5. Составление контура перераспределения ресурсов;
6. Определение min элемента в контуре перераспределения ресурсов;
7. Получение нового плана.
Описанная процедура повторяется несколько раз (итераций) пока не будет найдено оптимальное решение.
Существует несколько методов отыскания начального плана:
- метод северо-западного угла:
- метод min стоимости(элемента).
Вычислительный алгоритм метода потенциалов рассмотрим на примере решения конкретной задачи при 3-х пунктах отправления и 4-х пунктах назначения.
Дата добавления: 2019-12-09; просмотров: 682;











