Гомоморфные системы
А (гр.1) В (гр. 2)
х2 х2
а Dх2
х2 Dх1 х1
В системе А (гр. 1) мы можем определить в " момент времени координаты " точки, то есть точки а . При переходе от системы А к системе В можно точно определить квадрат, которому будут соответствовать координаты точки а. От системы В нельзя точно обратно перейти к системе А. Говорят, что система В гомоморфна системе А.
Система гомоморфна какой-то другой системе, если она получена из нее путем более грубого представления связей или координат.
Моделью называется система гомоморфная относительно реальной системы, т.е. модель – это некоторое упрощенное, грубое отображение реальной системы.
Классификация моделей.
1. Физические:
а) ассоциативные модели – понятие неизвестного через что-то известное.
б) аналоговые: они имитируют поведение реальной системы через аналогичные действия физических, пневматических и других приборов. Своеобразие этих моделей в том, что они узкоспециализированные, т. е. применяются для узкого круга объектов.
2. Математические модели – наиболее универсальный тип моделей. Здесь поведение реальной системы описывается математическими уравнениями. Экономико - математическая модель с помощью математического уравнения описывает поведение экономической системы. Для экономико - математической модели обычно характерно наличие целевой функций и большого числа ограничений.
Математические модели делятся по:
- учёту фактора времени:
· статические
· динамические
- наличию или отсутствию случайных факторов:
· детерминированные
· стохастические
- наличию сторон, принимающих решения:
· описательные (нет сторон, принимающих решения, модель даёт только описание процесса)
· нормативные (есть сторона(ы), есть цель и есть план)
- виду целевой функции и ограничений:
· линейные
· нелинейные
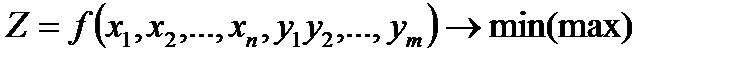
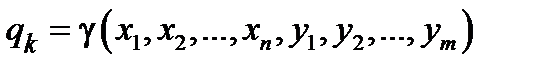
 Qk
Qk
x от 1 до n - управляемые переменные
y от 1 до m - неуправляемые(параметры), они заданны заранее и неизмененны.

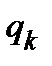
 - ограничения, накладываемые на задачу.
- ограничения, накладываемые на задачу.
Линейные модели: все зависимости выражены в линейной форме, т. е. искомые переменные даны в 1 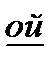 степени и не перемножаются друг на друга.
степени и не перемножаются друг на друга.
В не линейных моделях искомые переменные в целевой функции или в ограничениях могут быть в любой степени и они могут перемножаться друг на друга.
- по наличию ограничений:
· без ограничений
· с ограничениями.
Дата добавления: 2019-12-09; просмотров: 855;











