Основные теоремы линейного программирования.

1. Множество допустимых планов задач линейного программирования является выпуклым, (выпуклое множество-множество, которое вместе с 2-мя точками содержит и отрезок, содержащий эти точки.)

2. Если задача линейного программирования разрешима, то оптимальное значение целевой функции достигается, по крайней мере, в одной из вершин многогранника ограничений.

Если целевая функция достигает оптимального значения более чем в одной вершине, то она достигает такого же значения в любой точке отрезка, соединяющего эти вершины, и получается множество альтернативных оптимальных планов.

3. Если х = (х₁,х₂, …х_n) – это вершина многогранника ограничений, то векторы Аi в разложении х₁ А₁ + х₂ А₂ + …+х_n A_n = В, соответствующие положительным х_i, являются линейно-независимыми.

План х = (х₁,х₂, …х_n) называется опорным (допустимым, базисным), если векторы Аi входящие в разложение х₁ А₁ + х₂ А₂ + …+х_n A_n = В с (+) коэффициентами являются линейно независимыми.

Опорные планы соответствуют вершинам многогранника ограничений. m – векторов 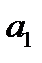, ,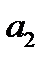…, 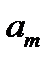линейно независимы, если из уравнения 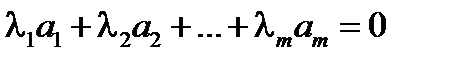, следует, что 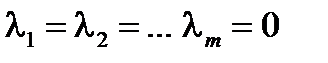, в противном случае векторы считаются линейнозависимыми.