Стандартный вид таблицы-матрицы.
| Потребители (пункты назначений) Поставщики (пункты отправлений) | B1 | B2 | B3 | B4 | Запасы Qi | ai |
| А1 | - | + | V | V | ||
| А2 | V | - | + | V | ||
| А3 | V + | V | - | |||
| Потребности Vj | ||||||
| bj |
Математическая постановка данной задачи:
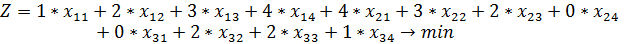
1. 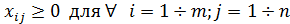
2. 
3. 
4. 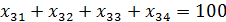
5. 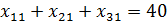
6. 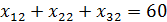
7. 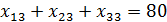
8. 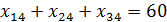
Начальный план составим с использованием метода северо-западного угла. Здесь заполнение матрицы начинается с верхней левой клетки и продолжается вправо и вниз.
Загрузим 1-ую клетку с индексом 11.
X11 = min (Q1; V1) = min(60, 40) = 40
X12 = min(  Q1; V2) = min(20; 60) = 20
Q1; V2) = min(20; 60) = 20
Для каждого расчёта потенциалов и нахождения оптимального плана число заполненных клеток должно быть равно m + n-1(m=3; n=4)
Значение целевой функции для начального плана рассчитаем по формуле:
Z = 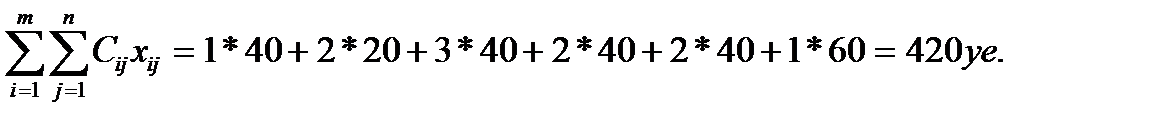
Расчёт потенциалов выполняется по заполненным клеткам из условия выполнения следующего равенства:
ai + bj = Cij
Первый потенциал принимается произвольно: а1 = 0
a1 + b1 = 1 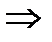 b1 = 1
b1 = 1
a1 + b2 = 2 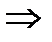 b2 = 2
b2 = 2
a2 + b2 = 3 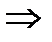 a2 = 1
a2 = 1
a2 + b3 = 2 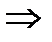 b3 = 1
b3 = 1
a3 + b3 = 2 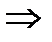 a3 = 1
a3 = 1
a3 + b4 = 1 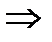 b4 = 0
b4 = 0
Признак оптимальности для метода потенциалов - это выполнение следующего неравенства:
для пустых клеток в оптимальном плане должно выполнятся
ai + bj 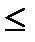 Cij
Cij
Если для всех пустых клеток данное неравенство выполняется, то план признаётся оптимальным.
Оптимальных планов с точки зрения различных сочетаний xij может быть несколько, но значение целевой функции у всех оптимальных планов будет одинаковым.
1-3 0+1<3 2-4 1+0 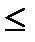 0!
0!  0=1
0=1
1-4 0+0<4 3-1 1+1 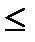 0!
0!  0=2
0=2
2-1 1+1<4 3-2 2+1 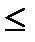 2!
2!  0=1
0=1
Для устранения нарушения оптимальности следует клетку с max нарушением из незаполненной сделать заполненной. Для этого строится контур перераспределения ресурсов. Этот контур представляет собой замкнутый многоугольник с вершинами в заполненных клетках за исключением клетки с вершиной max неоптимальности. Число вершин контура должно быть чётное и в каждом столбце(строке) – 2 вершины. Одна - загружается, другая- разгружается.
| Потребители (пункты назначений) Поставщики (пункты отправлений) | B1 | B2 | B3 | B4 | Запасы Qi | ai |
| А1 | V | V | ||||
| А2 | V | V | - | V + | -1 | |
| А3 | V | 0 + | - 1 | -1 | ||
| Потребности Vj | ||||||
| bj |
Чтобы узнать объём, который мы перенесли в клетку с max нарушением оптимальности, мы должны выбрать min объём из клеток контура помеченных знаком «-»
X min = min 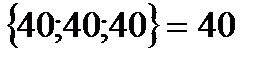
Недостающее количество заполненных клеток (до m + n - 1) заполняем условными нулями.
Далее рассчитываем новые значения потенциалов(а1=0)
по заполненным клеткам из равенства ai + bj = Cij.
Проверяем план на оптимальность.
Предварительно рассчитаем целевую функцию:
Z = 2*60+2*80+1*60=340у. е.
(1-3) 0+3=3 (2-2) -1+2<3
(1-4) 0+2<4 (2-4) -1+2<0
(2-1) -1+1<4 (3-2) -1+2<2
Нарушение в клетке 3-1, начиная с нее строим новый контур.
| Потребители (пункты назначений) Поставщики (пункты отправлений) | B1 | B2 | B3 | B4 | Запасы Qi | ai |
| А1 | ||||||
| А2 | -1 | |||||
| А3 | -1 | |||||
| Потребности Vj | ||||||
| bj |
Z = 2*60+2*20+60*2=280у. е.
1-3) 0+3=3 2-2) -1+2<3
1-4) 0+1<4 3-2) -1+2<2
2-1) -1+1<4 3-4) -1+ 1<1
По всем пустым клеткам выполняется условие ai+bj 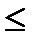 Cij
Cij  план оптимальный.
план оптимальный.
После получения оптимального плана проверяем ограничения.
60=60 40=40
20+60=80 60=60
40+60=100 20+60=80
60=60
Дата добавления: 2019-12-09; просмотров: 732;











