Дифференциальные уравнения равновесия жидкости

(уравнения Эйлера)

Рассмотрим равновесие жидкости (рис. 11). Возьмем точку А и выделим около нее прямоугольный параллелепипед со сторонами 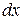, , 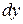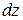. Обозначим внешние силы, отнесенные к единице массы через 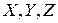. Внешними силами здесь будут:

- объемные, пропорциональные массе параллелепипеда;

- силы гидростатического давления, действующие на грани параллелепипеда со стороны окружающей жидкости.

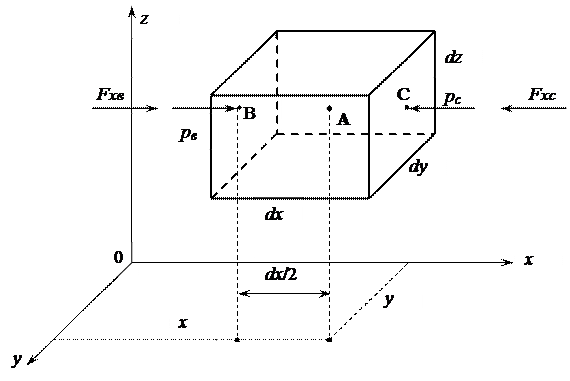Рисунок 11 – К выводу уравнений Эйлера

Рассмотрим сначала силы, действующие на жидкий параллелепипед по оси х.

Проекция объемных сил 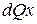на ось х будет равна:

;

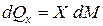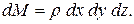
Следовательно, проекции объемных сил на все оси:

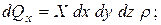
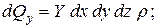
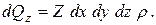
Гидростатическое давление в точке Вобозначим 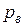, а в точке С – через 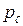. Если давление изменяется по линейному закону и непрерывно, тогда:

; ,

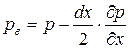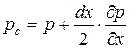где 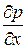– градиент гидростатического давления;

р – давление в точке А.

Силы, действующие на грани, равны:

;

.

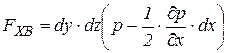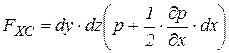Составим уравнение равновесия исследуемого нами жидкого объема относительно оси x:

;

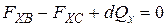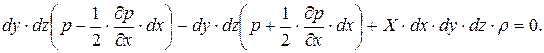
Уравнение равновесия после подстановки и преобразования сможем записать в виде:

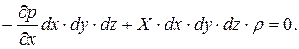
Окончательно уравнение равновесия относительно оси х будет иметь вид:

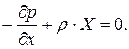
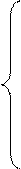Аналогично получим уравнение равновесия относительно осей y и z и запишем полную систему уравнений, которые называются уравнениями Эйлера.

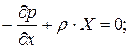
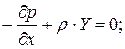
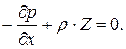
Впервые они были выведены в 1775 г. и выражают закон распределения гидростатического давления в дифференциальной форме.

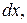
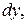
Для дальнейшего преобразования умножим каждое из уравнений системы на 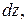соответственно

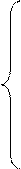
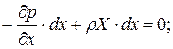
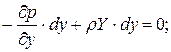
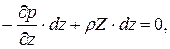
а сложив их почленно, получим следующее выражение:

.

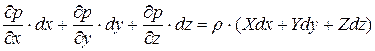Левая часть представляет полный дифференциал давления dp функции 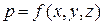. А так как левая часть – полный дифференциал функции, то и правая тоже. Только в этом случае уравнение может иметь смысл. Для этого

необходимо, чтобы существовала функция 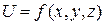, производные которой были равны:

; ; .

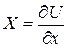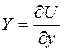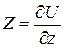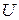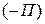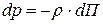Функция и обратная ей функция называются потенциальными. Следовательно, поле массовых сил потенциальное или ,где функция 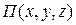выражает потенциальную энергию поля массовых сил (сил тяжести и инерции).

Интегрируя функцию 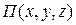для несжимаемой жидкости, получаем:

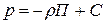или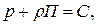

где С – постоянная интегрирования.

Для двух точек одного и того же объема данной однородной несжимаемой жидкости уравнение записывается в виде:

.

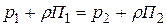Дадим определение поверхности равного давления: это поверхность, проведенная в покоящейся жидкости таким образом, что давление во всех ее точках одинаково, т. е. 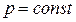. Поверхности равного давления обладают следующими основными свойствами:

- построенные для различных гидростатических давлений, они не имеют общих точек, т. е. не пересекаются;

- они всегда нормальны к направлению равнодействующей внешних объемных сил, приложенных к жидкости.