Основное уравнение гидростатики

Рассмотрим наиболее важный для практики частный случай равновесия жидкости, находящейся под действием только сил тяжести. Давление на

поверхности будем считать известным и равным 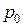, отличным от атмосферного (рис. 12).

Так как на жидкость действует только сила тяжести, то:

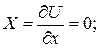
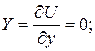
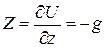
(ускорения по осям X и Y отсутствуют, а по оси Z ускорение свободного падения направлено вниз, поэтому ).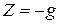

Подставим X, Y, Z в уравнения Эйлера (первые два уравнения обращаются в нуль) и получим:

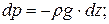
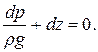
После интегрирования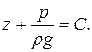

Для вычисления постоянной интегрирования С, подставим граничные условия и получим её значение:

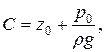
а подставив С в полученное выше уравнение, запишем:

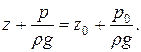
Уравнение выражает закон сохранения энергии в покоящейся жидкости. Сумма удельной потенциальной энергии положения z и удельной потенциальной энергии давления 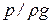есть величина постоянная во всех точках данной покоящейся жидкости.

Окончательно получим

.

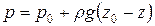А если учесть, ч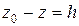то , то ,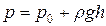

где h – глубина погружения точки в жидкость.

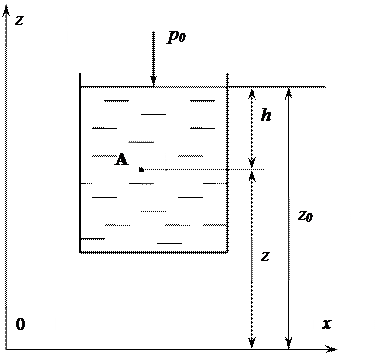Рисунок 12 – К основному уравнению гидростатики

Это уравнение выражает закон Паскаля: давление, приложенное к граничной поверхности жидкости. передается всем частицам этой жидкости по всем направлениям и без изменения.

Закон Паскаля используется при проектировании гидростатических машин, например, гидравлического пресса.