Физические свойства жидкости

Жидкость. Основные понятия

Жидкость представляет собой физическое тело, в котором силы межмолекулярного сцепления меньше, чем у твердых тел. Поэтому частицы жидкости легкоподвижны и приобретают как поступательное, так и вращательное движение, различают капельные и газообразные жидкости. Капельные жидкости характеризуются большим сопротивлением сжатию, практически полной несжимаемостью, малым сопротивлением растягивающим и касательным усилиям, что обусловлено незначительностью сил сцепления и сил трения между частицами жидкости и незначительной температурной расширяемостью. К капельным жидкостям относят воду, нефть, глицерин, бензин, спирт и т. д. Газообразные жидкости изменяют свой объем под влиянием указанных факторов в значительной степени, поэтому в гидравлике рассматривают обычно капельные жидкости, а газообразные рассматриваются в термодинамике и аэродинамике. При изменении давления или температуры жидкое тело может переходить в твердое или газообразное.

Таким образом, жидкость есть физическое тело, обладающее двумя отличительными свойствами:

1. Она весьма мало изменяет свой объем при изменении давления или температуры (сходна в этом с твердыми телами).

2. Она обладает текучестью, благодаря чему жидкость не имеет собственной формы и принимает форму того сосуда, в который она помещена (в этом она сходна с газом).

Жидкость настолько подвижна, что может течь под действием силы тяжести. Текучесть обусловлена тем, что в покоящемся состоянии она не способна сопротивляться внутренним касательным усилиям. Жидкость в покое не может иметь касательных напряжений и поэтому принимает форму сосуда, в который заключена.

Как показывает опыт, жидкости, встречающиеся в природе, столь мало изменяют объем при изменении давления р и температуры Т, что этим изменением можно пренебречь и рассматривать ее как абсолютно несжимаемое тело. В газах же этими свойствами пренебрегать нельзя.

В движущейся жидкости касательные напряжения имеют место. Именно при движении по поверхности скольжения жидких слоев друг по другу возникает трение, которое уравновешивает внутренние касательные силы.

Свойство жидкости, обусловливающее возникновение в ней при движении касательных напряжении, называется вязкостью.

При аналитических исследованиях для облегчения решения многих задач гидравлики часто пользуются понятием идеальной жидкости. Идеальной жидкостью называют воображаемую жидкость, которая характеризуется:

- абсолютной неизменяемостью объема при изменении давления или температуры (абсолютно несжимаемое тело);

- абсолютной подвижностью частиц, т. е. полным отсутствием вязкости, сил трения при ее движении.

Идеальная жидкость в отличие от реальной жидкости в природе не существует. Ее создают в воображении как чисто отвлеченную модель жидкой среды.

Но рассматривая вместо реальной жидкости идеальную, мы в ряде случаев не делаем большой ошибки. Только пренебрежение вязкостью может дать более или менее существенное расхождение с действительными условиями.

Физические свойства жидкости

Состояние и поведение применяемых в технике и производстве жидкостей находится в непосредственной зависимости от их физических свойств. Поэтому хотя физические свойства жидкостей изучаются в физике, но при расчетах в гидравлике пользуются некоторыми физическими характеристиками жидких тел, которые мы рассмотрим.

Плотность характеризует распределение массы 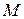жидкости или газа по объему 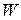. В произвольной точке А плотность

,

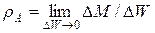где 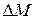– элементарная масса, заключенная в элементарном объеме 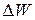, который стягивается в точку А.

Плотность однородной жидкости равна отношению массы жидкости 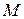к занимаемому ей объему :

.

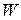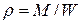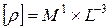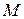Размерность плотности , где – единицы массы, а 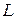– единицы длины. В системе СИ – 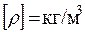в технической системе .

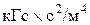Плотность жидкостей зависит от температуры и давления. Все жидкости, кроме воды, характеризуются уменьшением плотности при росте температуры. Плотность воды максимальна при t=4°С, в этом аномальность ее поведения. Для условий основных гидравлических расчетов плотность воды можно принимать равной 1000 .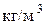

Удельный вес однородной жидкости определяется как отношение веса жидкости (газа) 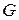к занимаемому объему :

.

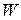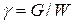Учитывая, что 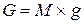, получим зависимость между плотностью и удельным весом, используемую в расчетах.

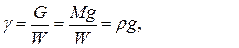то есть .

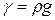Единицы удельного веса в системе СИ: .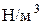

Относительным удельным весом жидкости называется отношение удельного веса жидкости 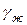при температуре t к удельному весу воды 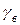при температуре 4°С:

.

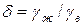Сжимаемость – свойство жидкостей изменять свой объем при изменении давления – характеризуется коэффициентом объемного сжатия (сжимаемости), представляющим относительное изменение объема жидкости, при изменении давления 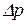на единицу:

,

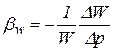где 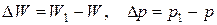– изменения объема и давления;

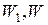– соответственно объемы жидкости при конечном 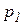и начальном р давлениях.

Знак (-) указывает на то, что положительному приращению давления (увеличению) 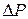соответствует отрицательное приращение (уменьшение) объема .

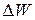Учитывая неизменность массы, можно представить 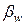несколько в ином виде:

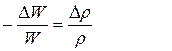и тогда ,

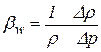где 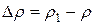является изменением плотности;

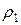– плотность при конечном давлении ;

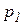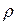– плотность при начальном давлении р.

То есть коэффициент объемного сжатия определяет также относительное изменение плотности при изменении давления на единицу.

Величина, обратная объемному коэффициенту сжатия, называется объемным модулем упругости жидкости.

,

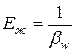или ,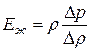

откуда .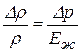

Эти уравнения выражают закон Гука для жидкостей.

Объемный модуль упругости жидкости 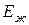зависит от температуры и давления, поэтому жидкости не всегда точно следуют закону Гука.

Сжимаемость жидкостей незначительна и в рассматриваемых в гидравлике явлениях, позволяет считать её несжимаемой, кроме отдельных случаев, которые оговариваются отдельно, например, гидравлический удар.

То есть это можно утверждать, когда давление незначительно. Но если бы вода была действительно абсолютно несжимаемой, то уровень воды в океанах поднялся примерно на 30 м.

Температурное расширение – это свойство жидкостей изменять свой объем при изменении температуры. Характеризуется температурным коэффициентом объемного расширения (температурного расширения), представляющим относительное изменение объема жидкости при изменении температуры на единицу и при постоянном давлении:

,

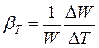где 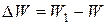– изменение объема жидкости,

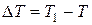– изменение температуры жидкости,

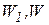– соответственно объемы жидкости при конечной 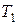и начальной 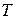температурах.

Вязкостьпредставляет собой свойство жидкости сопротивляться сдвигу (или скольжению) ее слоев. Вязкость проявляется в том, что при относительном перемещении слоев жидкости на поверхности их соприкосновения возникают силы сопротивления, называемые силами внутреннего трения, или силами вязкости. Происходит взаимное «торможение» и «ускорение» соседних слоев.

Силы внутреннего трения впервые обнаружены Ньютоном. Он установил пропорциональность между силой внутреннего трения, площадью соприкосновения и относительными скоростями перемещения слоев. Н. П. Петров в 80-годы ХIХ в. экспериментально подтвердил это и математически сформулировал в виде следующей зависимости, носящей название закона Ньютона-Петрова:

,

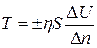где 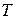– сила внутреннего трения слоев жидкости,

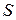– площадь соприкасающихся слоев,

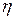– динамический коэффициент вязкости,

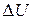– разность скоростей двух соседних слоев жидкости, расположенных на расстоянии 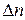друг от друга по нормали.

Поясним эти величины. Пусть между двумя пластинам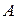и и 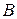, одна из которых неподвижна, залита жидкость (рис. 1). Пластина 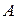, двигаясь со скоростью 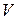, увлекает за собой прилежащий слой с такой же скоростью. Следующие слои будут двигаться с несколько другими скоростями, которые меньше 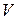из-за сопротивления жидкости.

Рисунок 1 – К определению силы внутреннего трения

Если слой 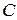имеет скорость 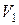, а слой 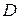– скорость 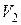, то 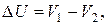а расстояние между ними по нормали .

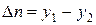Знак (+) или (-) в формуле Ньютона–Петрова для расчета силы внутреннего трения выбирается в зависимости от направления отсчета скоростей и расстояний (от движущейся пластины или от неподвижной). Сила трения при этом должна быть положительной.

Касательным напряжением 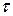называется сила 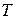, приходящаяся на единицу площади 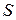, то есть:

.

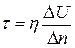Дальнейшие исследования показали, что численное значение касательного напряжения, возникающего вследствие действия силы внутреннего трения, равно:

,

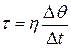где 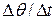– скорость деформационного сдвига.

Но с другой стороны, скорость деформационного сдвига равна градиенту скорости по нормали.

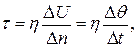то есть .

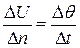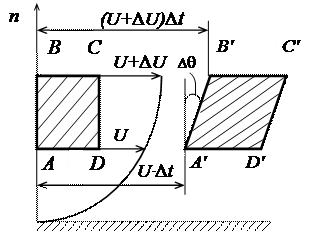
Рисунок 2 – Деформация жидкого прямоугольника

На рисунке 2 показана деформация жидкого прямоугольника ABCD. За время 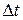он трансформируется в параллелограмм A'B'C'D'. Точка A пройдет путь 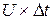, а точка B .

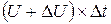Динамический коэффициент вязкости 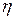имеет физический смысл – это сила трения, возникающая при единичных площади 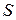и градиенте скорости .

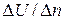Динамическая вязкость имеет размерность 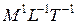или 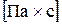в системе СИ (в системе 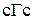– Пуаз; в технической системе кГс×с/м²).

В гидравлических расчетах, кроме динамической вязкости, широко используется кинематическая вязкость (кинематической вязкость называется, т. к. в размерность входят только кинематические, а не динамические величины). Динамическая 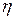и кинематическая вязкость 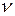связаны между собой следующим соотношением:

,

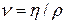где 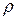– плотность жидкости.

Размерность 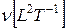в системе СИ 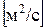(сГс - стокс=см²/с).

Отметим, что для жидкостей при увеличении температуры 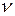и 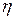уменьшаются примерно по экспоненциальному закону.

Жидкости, для которых справедлив закон Ньютона, называются ньютоновскими. Однако существуют жидкости, для которых связь между 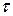и скоростью сдвиговой деформации выражаются другими соотношениями. Такие жидкости относятся к неньютоновским.